题目内容
已知点 为圆
为圆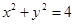 上的动点,且
上的动点,且 不在
不在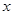 轴上,
轴上,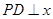 轴,垂足为
轴,垂足为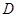 ,线段
,线段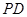 中点
中点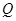 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点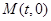
 任作一条与
任作一条与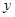 轴不垂直的直线
轴不垂直的直线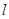 ,它与曲线
,它与曲线 交于
交于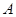 、
、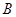 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在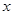 轴上存在定点
轴上存在定点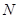 ,使得
,使得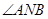 总能被
总能被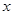 轴平分
轴平分
 为圆
为圆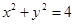 上的动点,且
上的动点,且 不在
不在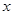 轴上,
轴上,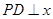 轴,垂足为
轴,垂足为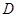 ,线段
,线段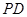 中点
中点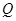 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点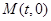
 任作一条与
任作一条与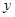 轴不垂直的直线
轴不垂直的直线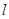 ,它与曲线
,它与曲线 交于
交于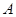 、
、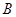 两点。
两点。(I)求曲线
 的方程;
的方程;(II)试证明:在
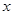 轴上存在定点
轴上存在定点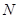 ,使得
,使得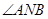 总能被
总能被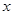 轴平分
轴平分(1)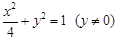 (2)见解析
(2)见解析
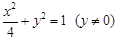 (2)见解析
(2)见解析第一问中设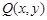 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点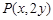 在圆
在圆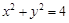 上,
上,
∴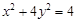 ,曲线
,曲线 的方程为
的方程为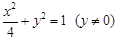
第二问中,设点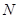 的坐标为
的坐标为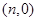 ,直线
,直线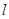 的方程为
的方程为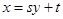 , ………………3分
, ………………3分
代入曲线 的方程
的方程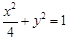 ,可得
,可得 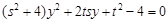
∵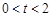 ,∴
,∴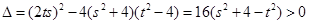
确定结论直线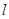 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点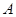 ,
,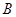 的坐标分别
的坐标分别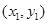 ,
, 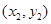 ,则
,则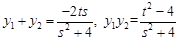 ,
,
要使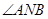 被
被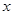 轴平分,只要
轴平分,只要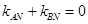 得到。
得到。
(1)设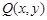 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点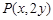 在圆
在圆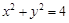 上,
上,
∴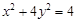 ,曲线
,曲线 的方程为
的方程为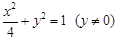 . ………………2分
. ………………2分
(2)设点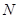 的坐标为
的坐标为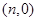 ,直线
,直线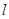 的方程为
的方程为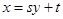 , ………………3分
, ………………3分
代入曲线 的方程
的方程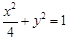 ,可得
,可得 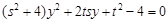 ,……5分
,……5分
∵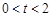 ,∴
,∴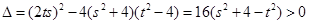 ,
,
∴直线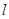 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点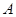 ,
,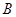 的坐标分别
的坐标分别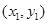 ,
, 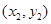 ,则
,则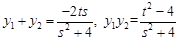 ,
,
要使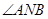 被
被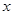 轴平分,只要
轴平分,只要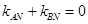 , ………………9分
, ………………9分
即 ,
,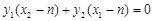 , ………………10分
, ………………10分
也就是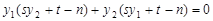 ,
,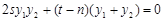 ,
,
即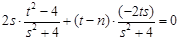 ,即只要
,即只要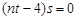 ………………12分
………………12分
当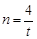 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而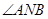 总能被
总能被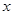 轴平分.
轴平分.
所以在x轴上存在定点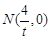 ,使得
,使得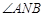 总能被
总能被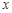 轴平分
轴平分
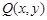 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点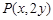 在圆
在圆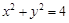 上,
上,∴
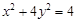 ,曲线
,曲线 的方程为
的方程为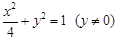
第二问中,设点
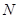 的坐标为
的坐标为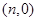 ,直线
,直线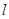 的方程为
的方程为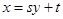 , ………………3分
, ………………3分 代入曲线
 的方程
的方程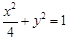 ,可得
,可得 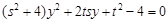
∵
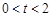 ,∴
,∴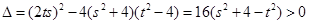
确定结论直线
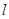 与曲线
与曲线 总有两个公共点.
总有两个公共点.然后设点
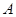 ,
,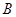 的坐标分别
的坐标分别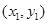 ,
, 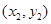 ,则
,则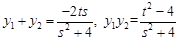 ,
, 要使
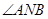 被
被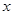 轴平分,只要
轴平分,只要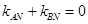 得到。
得到。(1)设
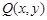 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点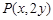 在圆
在圆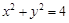 上,
上,∴
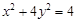 ,曲线
,曲线 的方程为
的方程为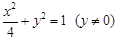 . ………………2分
. ………………2分 (2)设点
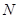 的坐标为
的坐标为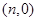 ,直线
,直线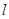 的方程为
的方程为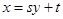 , ………………3分
, ………………3分 代入曲线
 的方程
的方程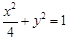 ,可得
,可得 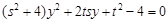 ,……5分
,……5分 ∵
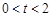 ,∴
,∴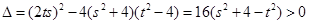 ,
,∴直线
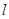 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)………………6分
设点
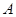 ,
,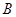 的坐标分别
的坐标分别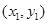 ,
, 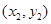 ,则
,则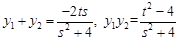 ,
, 要使
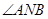 被
被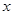 轴平分,只要
轴平分,只要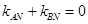 , ………………9分
, ………………9分即
 ,
,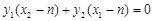 , ………………10分
, ………………10分也就是
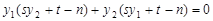 ,
,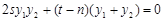 ,
, 即
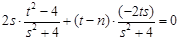 ,即只要
,即只要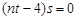 ………………12分
………………12分 当
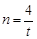 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而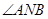 总能被
总能被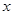 轴平分.
轴平分.所以在x轴上存在定点
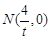 ,使得
,使得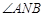 总能被
总能被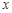 轴平分
轴平分
练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 中,椭圆
中,椭圆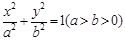 的左、右焦点分别为
的左、右焦点分别为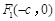 ,
,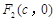 .已知
.已知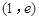 和
和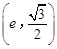 都在椭圆上,其中
都在椭圆上,其中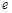 为椭圆的离心率.
为椭圆的离心率.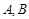 是椭圆上位于
是椭圆上位于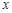 轴上方的两点,且直线
轴上方的两点,且直线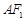 与直线
与直线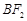 平行,
平行,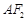 与
与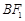 交于点P.
交于点P.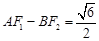 ,求直线
,求直线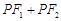 是定值.
是定值.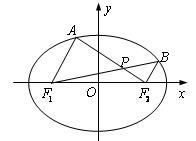
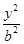 =1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
=1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
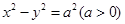 的左、右顶点分别为
的左、右顶点分别为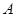 、
、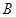 ,点
,点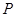 是第一象限内双曲线上的点.若直线
是第一象限内双曲线上的点.若直线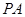 、
、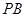 的倾斜角分别为
的倾斜角分别为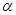 ,
,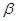 ,且
,且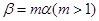 ,那么
,那么 是单位圆
是单位圆 上的任意一点,
上的任意一点, 是过点
是过点 轴垂直的直线,
轴垂直的直线, 是直线
是直线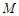 在直线
在直线 . 当点
. 当点 .
. 的直线交曲线
的直线交曲线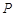 ,
,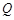 两点,其中
两点,其中 轴上的射影为点
轴上的射影为点 ,直线
,直线 交曲线
交曲线 . 是否存在
. 是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有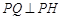 ?若存在,求
?若存在,求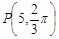 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
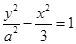 的两个焦点分别为
的两个焦点分别为 、
、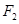 ,离心率为2.
,离心率为2.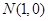 能否作出直线
能否作出直线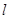 ,使
,使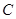 交于
交于 、
、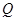 两点,且
两点,且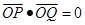 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.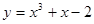 上点
上点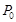 处的切线斜率为4,则点
处的切线斜率为4,则点