题目内容
在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的 倍后得到点Q(x,
倍后得到点Q(x, y),且满足
y),且满足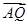 ·
·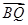 =1.
=1.
(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)过点B作斜率为- 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且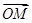 +
+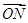 +
+ =
=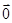 ,试求△MNH的面积.
,试求△MNH的面积.
 倍后得到点Q(x,
倍后得到点Q(x, y),且满足
y),且满足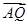 ·
·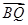 =1.
=1.(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)过点B作斜率为-
 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且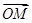 +
+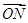 +
+ =
=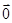 ,试求△MNH的面积.
,试求△MNH的面积. (1)曲线C的方程是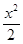 + y2=1 (2)S=
+ y2=1 (2)S=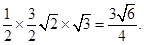
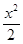 + y2=1 (2)S=
+ y2=1 (2)S=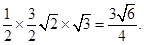
(I) 设点P的坐标为(x,y),则点Q的坐标为(x, y).然后求出
y).然后求出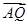 =(x+1,
=(x+1, y),
y), 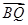 =(x-1,
=(x-1, y). 再对
y). 再对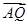 ·
·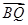 =1坐标化化简即可。
=1坐标化化简即可。
(II)先求出直线l的方程,然后与曲线C的方程联立,消去y,得到关于x的一元二次方程。
下面解题的关键是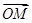 +
+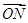 +
+ =
=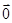 ,得
,得 =(- x1- x2,- y1- y2),即H(-1,-
=(- x1- x2,- y1- y2),即H(-1,- )
)
|MN|=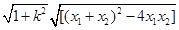 然后利用韦达定理求出|MN|,再利用点到直线的距离公式求出高,问题得解。
然后利用韦达定理求出|MN|,再利用点到直线的距离公式求出高,问题得解。
解:(Ⅰ)设点P的坐标为(x,y),则点Q的坐标为(x, y).
y).
依据题意,有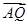 =(x+1,
=(x+1, y),
y), 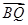 =(x-1,
=(x-1, y). ………………2分
y). ………………2分
∵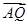 ·
·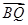 =1,∴x2-1+2 y2=1.∴动点P所在曲线C的方程是
=1,∴x2-1+2 y2=1.∴动点P所在曲线C的方程是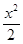 + y2="1" …………4分
+ y2="1" …………4分
(Ⅱ)因直线l过点B,且斜率为k=- ,故有l∶y=-
,故有l∶y=- (x-1)………………5分
(x-1)………………5分
联立方程组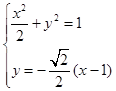 ,消去y,得2x2-2x-1=0. …………………7分
,消去y,得2x2-2x-1=0. …………………7分
设M(x1,y1)、N(x2,y2),可得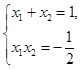 ,于是
,于是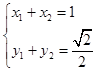 . ……………8分
. ……………8分
又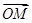 +
+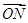 +
+ =
=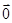 ,得
,得 =(- x1- x2,- y1- y2),即H(-1,-
=(- x1- x2,- y1- y2),即H(-1,- )……10分
)……10分
∴|MN|=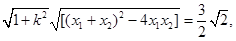 …………………………………12分
…………………………………12分
又l: x+2y-
x+2y- =0,则H到直线l的距离为d=
=0,则H到直线l的距离为d=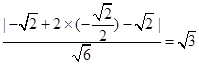
故所求MNH三角形的面积为S=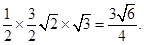
 y).然后求出
y).然后求出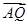 =(x+1,
=(x+1, y),
y), 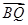 =(x-1,
=(x-1, y). 再对
y). 再对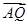 ·
·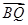 =1坐标化化简即可。
=1坐标化化简即可。(II)先求出直线l的方程,然后与曲线C的方程联立,消去y,得到关于x的一元二次方程。
下面解题的关键是
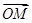 +
+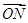 +
+ =
=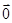 ,得
,得 =(- x1- x2,- y1- y2),即H(-1,-
=(- x1- x2,- y1- y2),即H(-1,- )
)|MN|=
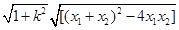 然后利用韦达定理求出|MN|,再利用点到直线的距离公式求出高,问题得解。
然后利用韦达定理求出|MN|,再利用点到直线的距离公式求出高,问题得解。解:(Ⅰ)设点P的坐标为(x,y),则点Q的坐标为(x,
 y).
y). 依据题意,有
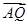 =(x+1,
=(x+1, y),
y), 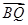 =(x-1,
=(x-1, y). ………………2分
y). ………………2分∵
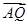 ·
·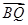 =1,∴x2-1+2 y2=1.∴动点P所在曲线C的方程是
=1,∴x2-1+2 y2=1.∴动点P所在曲线C的方程是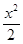 + y2="1" …………4分
+ y2="1" …………4分(Ⅱ)因直线l过点B,且斜率为k=-
 ,故有l∶y=-
,故有l∶y=- (x-1)………………5分
(x-1)………………5分联立方程组
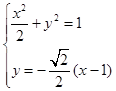 ,消去y,得2x2-2x-1=0. …………………7分
,消去y,得2x2-2x-1=0. …………………7分设M(x1,y1)、N(x2,y2),可得
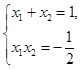 ,于是
,于是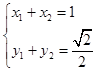 . ……………8分
. ……………8分又
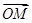 +
+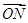 +
+ =
=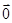 ,得
,得 =(- x1- x2,- y1- y2),即H(-1,-
=(- x1- x2,- y1- y2),即H(-1,- )……10分
)……10分∴|MN|=
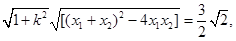 …………………………………12分
…………………………………12分又l:
 x+2y-
x+2y- =0,则H到直线l的距离为d=
=0,则H到直线l的距离为d=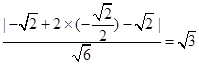
故所求MNH三角形的面积为S=
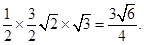

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,一个圆心为M,半径为
,一个圆心为M,半径为 的圆在
的圆在 是单位圆
是单位圆 上的任意一点,
上的任意一点, 是过点
是过点 轴垂直的直线,
轴垂直的直线, 是直线
是直线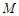 在直线
在直线 . 当点
. 当点 .
. 的直线交曲线
的直线交曲线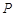 ,
,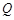 两点,其中
两点,其中 轴上的射影为点
轴上的射影为点 ,直线
,直线 交曲线
交曲线 . 是否存在
. 是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有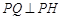 ?若存在,求
?若存在,求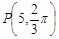 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
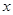 轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为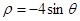 ,曲线F的参数方程为
,曲线F的参数方程为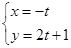 (t为参数)
(t为参数)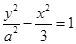 的两个焦点分别为
的两个焦点分别为 、
、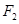 ,离心率为2.
,离心率为2.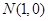 能否作出直线
能否作出直线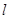 ,使
,使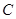 交于
交于 、
、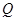 两点,且
两点,且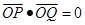 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.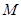 的坐标
的坐标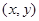 在其运动过程中
在其运动过程中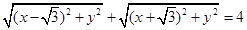 .
.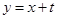 与
与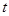 的值.
的值.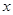 轴正半轴上一点
轴正半轴上一点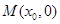 ,作圆
,作圆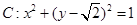 的两条切线,切点分别为
的两条切线,切点分别为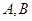 ,若
,若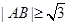 ,则
,则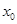 的最小值为( )
的最小值为( )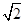
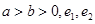 分别是圆锥曲线
分别是圆锥曲线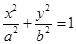 和
和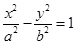 的离心率,设
的离心率,设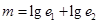 ,则
,则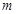 的取值范围是 .
的取值范围是 .