题目内容
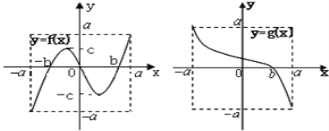
【题目】已知偶函数![]() 满足
满足![]() 且
且![]() ,当
,当![]() 时,
时,![]() ,关于
,关于![]() 的不等式
的不等式![]() 在
在![]() 上有且只有200个整数解,则实数
上有且只有200个整数解,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
判断f(x)在(0,8)上的单调性,根据对称性得出不等式在一个周期(0,8)内有4个整数解,再根据对称性得出不等式在(0,4)上有2个整数解,从而得出a的范围.
当0<x≤4时,f′(x)=![]() ,
,
令f′(x)=0得x=![]() ,
,
∴f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,4)上单调递减,
,4)上单调递减,
∵f(x)是偶函数,
∴f(x+4)=f(4﹣x)=f(x﹣4),
∴f(x)的周期为8,
∵f(x)是偶函数,且不等式f2(x)+af(x)>0在[﹣200,200]上有且只有200个整数解,
∴不等式在(0,200)内有100个整数解,
∵f(x)在(0,200)内有25个周期,
∴f(x)在一个周期(0,8)内有4个整数解,
(1)若a>0,由f2(x)+af(x)>0,可得f(x)>0或f(x)<﹣a,
显然f(x)>0在一个周期(0,8)内有7个整数解,不符合题意;
(2)若a<0,由f2(x)+af(x)>0,可得f(x)<0或f(x)>﹣a,
显然f(x)<0在区间(0,8)上无解,
∴f(x)>﹣a在(0,8)上有4个整数解,
∵f(x)在(0,8)上关于直线x=4对称,
∴f(x)在(0,4)上有2个整数解,
∵f(1)=ln2,f(2)=![]() =ln2,f(3)=
=ln2,f(3)=![]() ,
,
∴f(x)>﹣a在(0,4)上的整数解为x=1,x=2.
∴![]() ≤﹣a<ln2,
≤﹣a<ln2,
解得﹣ln2<a≤﹣![]() .
.
故答案为:D

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目