Question

【题目】如图，四边形为矩形，四边形为直角梯形，，，，，，.

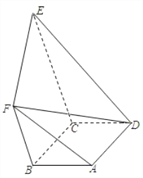
（1）求证：；

（2）求证：平面；

（3）若二面角的大小为，求直线与平面所成的角.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3)30°.

【解析】试题分析:（1）根据矩形性质得，再由条件，利用线面垂直判定定理得平面，即得结论（2）先根据线线平行得线面平行：平面，平面，再根据线面平行得面面平行：平面平面，即得线面平行（3）过作与的延长线垂直，则根据二面角定义得就是二面角的平面角，再根据面面垂直判定与性质定理得平面，即是直线与平面所成的角，最后通过解三角形得结果

试题解析：证明：（）∵四边形为矩形，∴，

又∵，，平面，，∴平面，

∵平面，∴．

（）∵，平面，平面，∴平面．

∵四边形是矩形，∴，又平面，

平面，∴平面，

又，平面，，∴平面平面，

∵平面，∴平面．

（）过作与的延长线垂直，是垂足，连结．

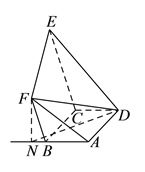
∵，，∴就是二面角的平面角，

∴，，∴，，

∵，，，∴．

∵平面，平面，

∴平面平面，又平面平面，，

∴平面，

∴是直线与平面所成的角，

∴，∴，

∴直线与平面所成的角为．