题目内容
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
【答案】(1) 当![]() 时,函数
时,函数![]() 的单调减区间是
的单调减区间是![]() ;单调增区间是
;单调增区间是![]() ;当
;当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() ;无单调减区间;当
;无单调减区间;当![]() 时,函数
时,函数![]() 的单调减区间是
的单调减区间是![]() ;单调增区间是
;单调增区间是![]() .(2) 存在整数
.(2) 存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为0.
的最小值为0.
【解析】试题分析:
本题考查用导数讨论函数的单调性和用导数解决函数中的能成立问题.(1)求导后根据导函数的符号判断函数的单调性.(2)由题意只需求出函数![]() 的最小值即可,根据函数的单调性求解即可.
的最小值即可,根据函数的单调性求解即可.
试题解析:
⑴由题意得函数的定义域为![]() .
.
∵![]() ,
,
∴![]() ,
,
①当![]() 时,
时,
则当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
②当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 上单调递增.
上单调递增.
③当![]() 时,
时,
则当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
综上,当![]() 时,
时, ![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,在
,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴函数![]() 单调递增,
单调递增,
又![]() ,
, ![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
且当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
所以![]() ,
,
设![]() ,
,
则![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() .
.
若关于![]() 的不等式
的不等式![]() 有解,则
有解,则![]() ,
,
又![]() 为整数,所以
为整数,所以![]() .
.
所以存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为0.
的最小值为0.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
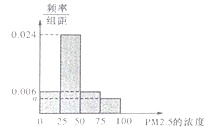
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
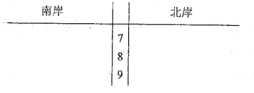
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.