Question

【题目】定义域和值域均为[-a，a]的函数y=和y=g（x）的图象如图所示，其中a＞c＞b＞0，给出下列四个结论正确结论的是（　　 ）

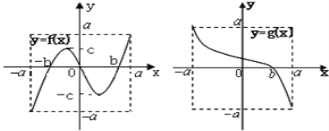
A.方程f[g（x）]=0有且仅有三个解B.方程g[f（x）]=0有且仅有三个解

C.方程f[f（x）]=0有且仅有九个解D.方程g[g（x）]=0有且仅有一个解

Answer 1

【答案】AD

【解析】

根据给定的函数的图象，结合函数的单调性，逐项判定，即可求解，得到答案。

由图象可知对于函数，当时，方程有一解，当时，方程有两解，当时方程由三解，当时，方程有两解，当时，方程有一解，对于函数，由图象可知，函数为单调递减函数，当，方程有唯一解。

对于A中，设，则由，即，此时方程有三个的值，即有三个不同的值，又由函数为单调递减函数，所以方程有三个不同的解，所以是正确的；

对于B中，设，则由，即，此时只有唯一的解，即方程，此时可能有一解、两解或三解，所以不正确；

对于C中，设，则由，即，此时或或，

则方程可能有5个解或7个解，或9个解，所以不正确；

对于D中，设，则由，即，此时，对于方程，只有唯一的解，所以是正确的。

故选：AD。