题目内容
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
【答案】(1)![]() .
.![]() .(2)1.
.(2)1.
【解析】【试题分析】(1) ![]() 展开后利用公式直接转化为直角坐标方程.对
展开后利用公式直接转化为直角坐标方程.对![]() 消去
消去![]() 后得到直角坐标方程.(2)求出直线
后得到直角坐标方程.(2)求出直线![]() 的参数方程,代入抛物线,利用直线参数的几何意义求得
的参数方程,代入抛物线,利用直线参数的几何意义求得![]() 的值.
的值.
【试题解析】
(1)由![]() ,得
,得![]() ,
,
令![]() ,
, ![]() ,得
,得![]() .
.
因为![]() ,消去
,消去![]() 得
得![]() ,
,
所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线
,曲线![]() 的普通方程为
的普通方程为![]() .
.
(2)点![]() 的直角坐标为
的直角坐标为![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
设直线![]() 的参数方程为
的参数方程为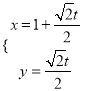 ,(
,( ![]() 为参数),代入
为参数),代入![]() ,得
,得![]() .
.
设点![]() 对应的参数分别为
对应的参数分别为![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
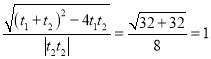 .
.

练习册系列答案
相关题目



