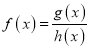题目内容
【题目】已知定义在区间(0,+∞)上的函数f(x)满足![]() =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)证明:f(x)为单调递减函数.
(2)若f(3)=-1,求f(x)在[2,9]上的最小值.
【答案】(1)见解析(2)-2
【解析】
(1)任取任取x1,x2∈(0,+∞),且x1>x2,进而可得![]() >1,接下来结合已知即可确定
>1,接下来结合已知即可确定![]() 与
与![]() 的大小关系,从而证得结果;
的大小关系,从而证得结果;
(2)由(1)的结论可知![]() 的最小值是
的最小值是![]() ,接下来结合已知可得
,接下来结合已知可得![]() ,据此即可求得
,据此即可求得![]() 的值,得到结果.
的值,得到结果.
解:(1)证明:任取x1,x2∈(0,+∞),且x1>x2,
则![]() >1,由于当x>1时,f(x)<0,
>1,由于当x>1时,f(x)<0,
所以f![]() <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,
因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(2)因为f(x)在(0,+∞)上是单调递减函数,
所以f(x)在[2,9]上的最小值为f(9).
由f![]() =f(x1)-f(x2)得,
=f(x1)-f(x2)得,
f![]() =f(9)-f(3),而f(3)=-1,
=f(9)-f(3),而f(3)=-1,
所以f(9)=-2.
所以f(x)在[2,9]上的最小值为-2.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】2019年6月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”的关注程度,某机构随机抽取了年龄在20—70岁之间的100人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() 。
。
关注 | 不关注 | 合计 | |
年轻人 | 30 | ||
中老年人 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有99﹪的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄有关?
列联表,并判断能否有99﹪的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄有关?
(2)现已经用分层抽样的办法从中老年人中选取了6人进行问卷调查,若再从这6人中选取3人进行面对面询问,记选取的3人中关注“中国湖北(潜江)龙虾节”的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
附:参考公式![]() 其中
其中![]() 。
。
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6635 | 10.828 |