题目内容
【题目】已知函数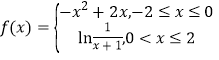 ,若
,若![]() 的图象与
的图象与![]() 轴有
轴有![]() 个不同的交点,则实数
个不同的交点,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】试题分析:化简 ,从而化g(x)=|f(x)|﹣ax﹣a的图象与x轴有3个不同的交点为函数|f(x)|与函数y=ax+a的图象有3个不同的交点;作函数的图象,由数形结合求实数a的取值范围.
,从而化g(x)=|f(x)|﹣ax﹣a的图象与x轴有3个不同的交点为函数|f(x)|与函数y=ax+a的图象有3个不同的交点;作函数的图象,由数形结合求实数a的取值范围.
详解:
∵ ,
,
∴|f(x)|=![]() ,
,
∵g(x)=|f(x)|﹣ax﹣a的图象与x轴有3个不同的交点,
∴函数|f(x)|与函数y=ax+a的图象有3个不同的交点;
作函数|f(x)|与函数y=ax+a的图象如下,
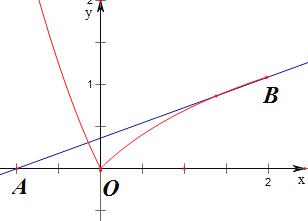
图中A(﹣1,0),B(2,ln3),
故此时直线AB的斜率k=![]() ;
;
当直线AB与f(x)=ln(x+1)相切时,设切点为(x,ln(x+1));
则![]() =
=![]() ,
,
解得,x=e﹣1;
此时直线AB的斜率k=![]() ;
;
结合图象可知,
![]() ≤a<
≤a<![]() ;
;
故答案为:![]() ≤a<
≤a<![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目



