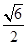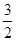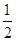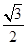题目内容
曲线C上任一点到点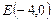 ,
,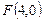 的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,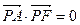 .
.
(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)以曲线C的中心为圆心,AB为直径作圆O,过点P的直线l截圆O的弦MN长为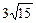 ,求直线l的方程.
,求直线l的方程.
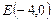 ,
,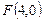 的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,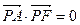 .
.(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)以曲线C的中心为圆心,AB为直径作圆O,过点P的直线l截圆O的弦MN长为
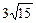 ,求直线l的方程.
,求直线l的方程.(Ⅰ)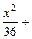
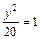
(Ⅱ)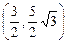
(Ⅲ)所求的直线l的方程为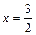 或
或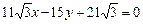
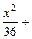
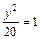
(Ⅱ)
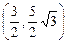
(Ⅲ)所求的直线l的方程为
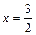 或
或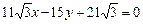
(Ⅰ)设G是曲线C上任一点,依题意,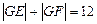
∴曲线C是以E、F为焦点的椭圆,且椭圆的长半轴a=6,半焦距c=4,
∴短半轴b=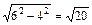 ,
,
∴所求的椭圆方程为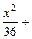
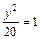 ;
;
(Ⅱ)由已知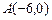 ,
,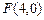 ,设点P的坐标为
,设点P的坐标为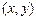 ,则
,则
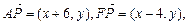 由已知得
由已知得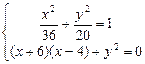
则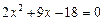 ,解之得
,解之得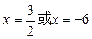 ,
,
由于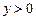 ,所以只能取
,所以只能取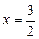 ,于是
,于是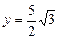 ,
,
所以点P的坐标为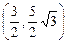 ;
;
(Ⅲ)圆O的圆心为(0,0),半径为6,其方程为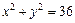 ,
,
若过P的直线l与x轴垂直,则直线l的方程为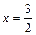 ,这时,圆心到l的距离
,这时,圆心到l的距离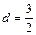 ,
,
∴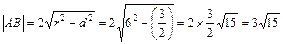 ,符合题意;
,符合题意;
若过P的直线l不与x轴垂直,设其斜率为k,则直线l的方程为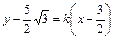 ,
,
即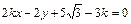 ,这时,圆心到l的距离
,这时,圆心到l的距离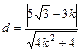
∴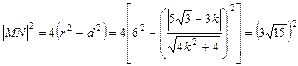 ,
,
化简得,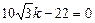 ,∴
,∴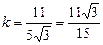 ,
,
∴直线l的方程为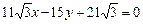 ,
,
综上,所求的直线l的方程为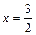 或
或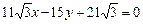
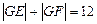
∴曲线C是以E、F为焦点的椭圆,且椭圆的长半轴a=6,半焦距c=4,
∴短半轴b=
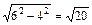 ,
,∴所求的椭圆方程为
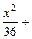
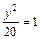 ;
;(Ⅱ)由已知
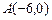 ,
,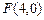 ,设点P的坐标为
,设点P的坐标为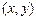 ,则
,则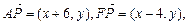 由已知得
由已知得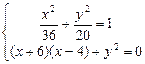
则
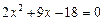 ,解之得
,解之得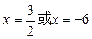 ,
,由于
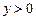 ,所以只能取
,所以只能取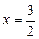 ,于是
,于是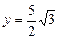 ,
,所以点P的坐标为
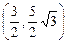 ;
;(Ⅲ)圆O的圆心为(0,0),半径为6,其方程为
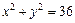 ,
,若过P的直线l与x轴垂直,则直线l的方程为
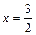 ,这时,圆心到l的距离
,这时,圆心到l的距离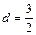 ,
,∴
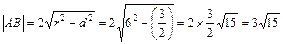 ,符合题意;
,符合题意;若过P的直线l不与x轴垂直,设其斜率为k,则直线l的方程为
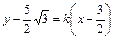 ,
,即
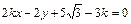 ,这时,圆心到l的距离
,这时,圆心到l的距离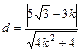
∴
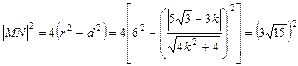 ,
,化简得,
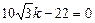 ,∴
,∴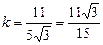 ,
,∴直线l的方程为
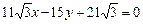 ,
,综上,所求的直线l的方程为
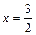 或
或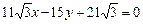

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
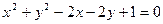 相切的直线
相切的直线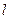 交x轴、y轴于A、B两点,O为坐标原点,且|OA|=
交x轴、y轴于A、B两点,O为坐标原点,且|OA|=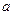 ,
,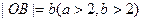 。
。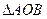 面积的最小值。
面积的最小值。

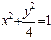
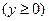 的铁皮截取一个以短轴
的铁皮截取一个以短轴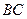 为底的等腰梯形
为底的等腰梯形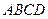 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形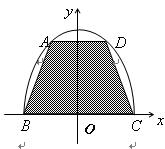
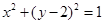 相切,且在每坐标轴上截距相等的距离有( )
相切,且在每坐标轴上截距相等的距离有( )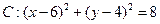 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.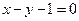 相切于点 B(2,1).则圆C的方程为
相切于点 B(2,1).则圆C的方程为 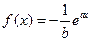 在x=0处的切线
在x=0处的切线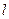 与圆
与圆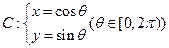 相离,则
相离,则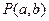 与圆
与圆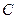 的位置关系是:
的位置关系是: 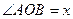 ,当直
,当直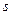 关于
关于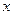 的函数
的函数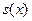 =____________________.
=____________________.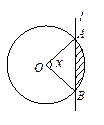
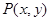 在直线
在直线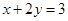 上移动,当
上移动,当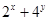 取得最小值时,过点
取得最小值时,过点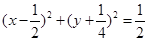 的切线,则此切线段的长度为( )
的切线,则此切线段的长度为( )