题目内容
(本小题满分12分)如图,用一块形状为半椭圆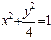
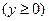 的铁皮截取一个以短轴
的铁皮截取一个以短轴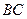 为底的等腰梯形
为底的等腰梯形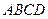 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形 的面积最大?
的面积最大?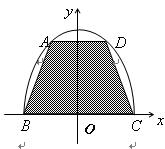
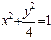
 的铁皮截取一个以短轴
的铁皮截取一个以短轴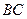 为底的等腰梯形
为底的等腰梯形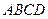 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形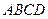 的面积最大?
的面积最大?
只需分别作 的中垂线与上半椭圆交于
的中垂线与上半椭圆交于 ,这样的等腰梯形的面积最大.
,这样的等腰梯形的面积最大.
 的中垂线与上半椭圆交于
的中垂线与上半椭圆交于 ,这样的等腰梯形的面积最大.
,这样的等腰梯形的面积最大.设 点坐标为
点坐标为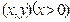 ,由点
,由点 在椭圆上知
在椭圆上知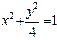
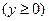 ,
,
得
∴等腰梯形 的面积为
的面积为
 (2分)
(2分)
∴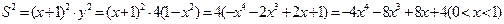
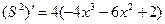 ,令
,令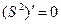 ,
,
得 ,
,
∵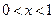 ,∴
,∴ , (6分)
, (6分)
又当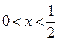 时,
时,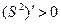 ;当
;当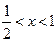 时,
时, ,
,
∴在区间 上,
上,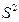 有唯一的极大值点
有唯一的极大值点 , (8分)
, (8分)
∴当 时,
时,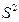 有最大值为
有最大值为 ;
;
即当 时,
时,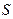 有最大值为
有最大值为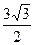 . (10分)
. (10分)
因此只需分别作 的中垂线与上半椭圆交于
的中垂线与上半椭圆交于 ,这样的等腰梯形的面积最大.
,这样的等腰梯形的面积最大.
(12分)
 点坐标为
点坐标为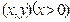 ,由点
,由点 在椭圆上知
在椭圆上知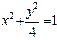
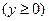 ,
,得

∴等腰梯形
 的面积为
的面积为 (2分)
(2分)∴
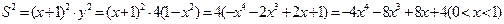
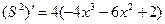 ,令
,令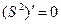 ,
,得
 ,
,∵
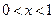 ,∴
,∴ , (6分)
, (6分)又当
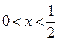 时,
时,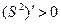 ;当
;当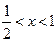 时,
时, ,
,∴在区间
 上,
上,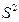 有唯一的极大值点
有唯一的极大值点 , (8分)
, (8分)∴当
 时,
时,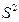 有最大值为
有最大值为 ;
;即当
 时,
时,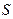 有最大值为
有最大值为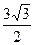 . (10分)
. (10分)因此只需分别作
 的中垂线与上半椭圆交于
的中垂线与上半椭圆交于 ,这样的等腰梯形的面积最大.
,这样的等腰梯形的面积最大.(12分)

练习册系列答案
相关题目
 通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线
通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线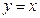 上。
上。 的方程;
的方程;
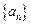 满足:
满足: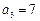 ,
,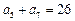 .
.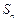 .
.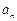 及
及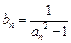 (
(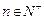 ),求数列
),求数列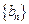 的前n项和
的前n项和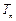 .
. 和y轴都相切.
和y轴都相切.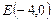 ,
,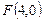 的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,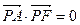 .
.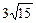 ,求直线l的方程.
,求直线l的方程. +
+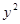 =1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )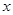 ;
; 经过
经过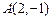 和直线
和直线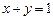 相切,且圆心在直线
相切,且圆心在直线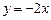 上.
上. 经过圆
经过圆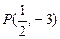 与圆
与圆 两点,当弦
两点,当弦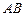 被点
被点 平分时,求直线
平分时,求直线 已知圆的直径
已知圆的直径 ,
,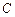 为圆上一点,过
为圆上一点,过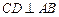 于
于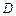 (
( ),若
),若 ,则
,则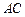 的长为 .
的长为 . 在
在 上的单调递减区间为 .
上的单调递减区间为 .