题目内容
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() ,
, ![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值

【答案】(1)见解析;(2)![]()
【解析】分析:第一问首先要分析清在翻折的时候哪些量是不变的,哪些量是变化的,之后借助于勾股定理证得![]() ,再利用题的条件,证得相关的垂直关系,之后借助于线面垂直的判定定理证得结果;第二问建立空间直角坐标系,利用空间向量求得线面角的正弦值.
,再利用题的条件,证得相关的垂直关系,之后借助于线面垂直的判定定理证得结果;第二问建立空间直角坐标系,利用空间向量求得线面角的正弦值.
详解:(1)证明:设正方形![]() 的边长为4,由图1知,
的边长为4,由图1知,![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,即
,即![]()
由题意知,在图2中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() 平面
平面![]()
(2)解:由(1)知![]() 平面
平面![]() ,则建立如图所示空间直角坐标系,过点
,则建立如图所示空间直角坐标系,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,在
,在![]() 中,
中,![]() ,
,![]()
![]() ,从而
,从而![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则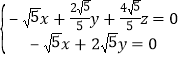 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() ,
,![]()
![]() .
.![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数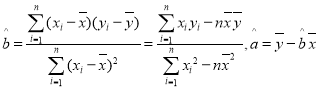 .
.