题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)是否存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
【答案】(1)答案见解析;(2)答案见解析.
【解析】分析:第一问先将函数![]() 的解析式确定,接着写出函数的定义域,之后对函数求导,对a进行讨论,确定导数的符号,从而求得函数的单调区间,第二问假设存在,之后将其转化为最值问题,借用导数研究函数的图像的走向,从而确定函数的最值,最后求得结果.
的解析式确定,接着写出函数的定义域,之后对函数求导,对a进行讨论,确定导数的符号,从而求得函数的单调区间,第二问假设存在,之后将其转化为最值问题,借用导数研究函数的图像的走向,从而确定函数的最值,最后求得结果.
详解:(1)由已知得![]() ,
,![]() 的定义域为
的定义域为![]() ,
,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上单调递减;
上单调递减;
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
(i)当![]() (
(![]() ),即
),即![]() 时,所以
时,所以![]() (
(![]() ),
),
所以函数![]() 在
在![]() 上单调递增;
上单调递增;
(ii)当![]() ,即
,即![]() 时,在
时,在![]() 和
和![]() 上函数
上函数![]() ,在
,在![]() 上函数
上函数![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(iii)当![]() ,即
,即![]() 时,在
时,在![]() 和
和![]() 上函数
上函数![]() ,在
,在![]() 上函数
上函数![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() ,
,
记![]() ,只需
,只需![]() .
.
又![]() ,
,
记![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,即
,即![]() ,且
,且![]() ,故
,故![]() 的最小整数值为3,
的最小整数值为3,
所以存在最小整数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立.
恒成立.

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】某企业有![]() ,
,![]() 两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从
两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从![]() ,
,![]() 两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
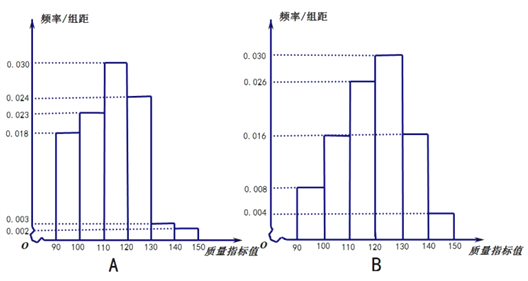
(1)根据频率分布直方图,分别求出![]() 分厂的质量指标值的众数和中位数的估计值;
分厂的质量指标值的众数和中位数的估计值;
(2)填写![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为这两个分厂的产品质量有差异?
的把握认为这两个分厂的产品质量有差异?
优质品 | 非优质品 | 合计 | |
| |||
| |||
合计 |
(3)(i)从![]() 分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
(ii)将频率视为概率,从![]() 分厂中随机抽取10件该产品,记抽到优质品的件数为
分厂中随机抽取10件该产品,记抽到优质品的件数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |