题目内容
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】试题分析:(1)根据已知条件求出![]() ,对参数
,对参数![]() 的取值进行分类讨论,即可求出
的取值进行分类讨论,即可求出![]() 的单调区间.
的单调区间.
(2)将不等式![]() 转化为
转化为![]() .令
.令![]() ,
,![]() .通过导数研究
.通过导数研究![]() 的单调性,可知
的单调性,可知![]() ,即可求出实数
,即可求出实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,无减区间.
,无减区间.
当![]() 时,令
时,令![]() ,
,![]() ,
,
列表:
|
|
|
|
| + | - | + |
|
|
|
|
由表可知,当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() 和
和![]() ,
,
递减区间为![]() .
.
(Ⅱ)∵![]() ,
,
∴由条件,![]() 对
对![]() 成立.
成立.
令![]() ,
,![]() ,
,
∴![]()
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
故![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,
,
∴![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
点晴:本题考查的用导数研究函数的单调性和用导数解决不等式恒成立问题.研究单调性问题,首先看导函数对应的方程能否因式分解,否则的话需要对其判别式,
进行分别讨论,![]() 时原函数单调,
时原函数单调,![]() ,需要对方程的根和区间的端点大小进行比较;第二问中的不等式恒成立问题,首选变量分离转化为确定的函数求最值即可.
,需要对方程的根和区间的端点大小进行比较;第二问中的不等式恒成立问题,首选变量分离转化为确定的函数求最值即可.

【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=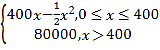 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如右表.
组 号 | 年龄 | 访谈 人数 | 愿意 使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式:![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |