题目内容
【题目】北方某市一次全市高中女生身高统计调查数据显示：全市20000名高中女生的身高（单位：
）服从正态分布
.现从某高中女生中随机抽取50名测量身高，测量发现被测学生身高全部在
和
之间，现将测量结果按如下方式分成6组：第1组
，第2组
，…，第6组
，下图是按上述分组方法得到的频率分布直方图.
（1）求这50名女生身高不低于172的人数；
（2）在这50名女生身高不低于172的人中任意抽取2人，将该2人中身高排名（从高到低）在全市前260名的人数记为
，求的数学期望.
参数数据：
，
.
【答案】(1)10.
(2)
.
【解析】
分析：（1）先求后3组频率，再求50名女生身高不低于172cm的人数.(2)先求随机变量
可取0，1，2，再求其概率，最后写出其分布列，求出其数学期望.
详解：（1）由直方图知，后3组频率为
，
所以人数为
，即这50名女生身高不低于172cm的人数为10人；
（2）∵
∴
∴
，则全市高中女生的身高在180cm以上的有260人，这50人中180cm以上的有2人.
随机变量可取0，1，2，
于是
X | 0 | 1 | 2 |
P |
|
|
|
∴
.
ξ | x1 | x2 | … | xn | … |
P | p1 | p2 | … | pn | … |
【题目】某中学共有5000人，其中男生3500人，女生1500人，为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关，现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据（单位：小时），其频率分布直方图如下：
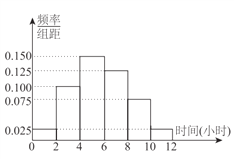
附：
，其中
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中，有60位女生的每周平均体育锻炼时间超过4小时，根据独立性检验原理，我们（ ）
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
