题目内容
4.函数f(x)=-$\frac{1-{2}^{x}}{lo{g}_{2}(x-1)}$的定义域为{x|x>1且x≠2}.分析 由对数的真数大于零和分母不为零列出不等式组,求出x的范围再用集合或区间的形式表示出来.
解答 解:要使原式有意义,则$\left\{\begin{array}{l}{x-1>0}\\{{log}_{2}^{(x-1)}≠0}\end{array}\right.$,
解得x>1且x≠2,
所以函数的定义域是{x|x>1且x≠2},
故答案为:{x|x>1且x≠2}.
点评 本题考查了函数的定义域的求法,掌握求函数的定义域的法则是解题的关键,属于基础题.

练习册系列答案
相关题目
14.一个几何体的三视图如图所示,该几何体的体积为( )


| A. | 4$\sqrt{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
15.如图△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,则BD的长为( )


| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
19.若集合P={y|y≥0},且P∪Q=Q,则集合Q可能是( )
| A. | {y|y=x2+1} | B. | {y|y=2x} | C. | {y|y=lgx} | D. | ∅ |
13.已知i为虚数单位,复数z满足z(2-i)=10+5i,则z等于( )
| A. | 3+4i | B. | 3-4i | C. | -3+4i | D. | -3-4i |
 某市教育部门对甲校四年级学生进行体育学科测试,随机抽取15名学生的测试成绩,绘制茎叶图如图:
某市教育部门对甲校四年级学生进行体育学科测试,随机抽取15名学生的测试成绩,绘制茎叶图如图: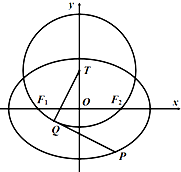 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.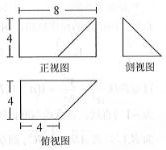 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.