题目内容
14.已知各项均为正数的数列{an}的前n项和为sn,a1=1,4sn=a${\;}_{n+1}^{2}$-4n-1,n∈N*.(1)求a2,a3的值;
(2)求数列{an}的通项公式;
(3)证明:n∈N*,有$\frac{1}{{a}_{1}{a}_{2}+1}$+$\frac{1}{{a}_{2}{a}_{3}+1}$+$\frac{1}{{a}_{3}{a}_{4}+1}$+…+$\frac{1}{{a}_{n}{a}_{n+1}+1}$<$\frac{1}{2}$.
分析 (1)利用4sn=a${\;}_{n+1}^{2}$-4n-1,直接求出a2=3,a3=5.
(2)通过4sn=a${\;}_{n+1}^{2}$-4n-1,写出4sn-1=a${\;}_{n}^{2}$-4(n-1)-1,推出a${\;}_{n+1}^{2}$=$({a}_{n}+2)^{2}$,n≥2,说明数列{an}是首项为1,公差为2的等差数列,求出an.
(3)利用通项$\frac{1}{{a}_{n}{a}_{n+1}+1}$放大为$\frac{1}{{a}_{n}{a}_{n+1}}$,然后利用裂项求和证明即可.
解答 解:(1)由4sn=a${\;}_{n+1}^{2}$-4n-1得4s1=a22-4-1,
因为an>0,a1=1,所以a2=$\sqrt{4{a}_{1}+5}$=3,所以a2=3,
据而可得a3=5--------(2分).
(2)4sn=a${\;}_{n+1}^{2}$-4n-1-----(1)
当n≥2,4sn-1=a${\;}_{n}^{2}$-4(n-1)-1-----(2)
由(1)-(2)得4an=a${\;}_{n+1}^{2}$-a${\;}_{n}^{2}$-4,即a${\;}_{n+1}^{2}$=$({a}_{n}+2)^{2}$,n≥2
因为an>0,所以an+1=an+2,an+1-an=2,(n≥2),
又a2-a1=2,所以数列{an}是首项为1,公差为2的等差数列,
所以an=2n-1.-----------(8分)(或用数学归纳法)
(3)$\frac{1}{{a}_{n}{a}_{n+1}+1}$<$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$$(\frac{1}{2n-1}-\frac{1}{2n+1})$,
所以$\frac{1}{{a}_{1}{a}_{2}+1}$+$\frac{1}{{a}_{2}{a}_{3}+1}$+$\frac{1}{{a}_{3}{a}_{4}+1}$+…+$\frac{1}{{a}_{n}{a}_{n+1}+1}$<$\frac{1}{2}$$(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$=$\frac{1}{2}-\frac{1}{4n+2}<\frac{1}{2}$,-------------(14分).
点评 本题考查数列的递推关系式的应用,通项公式的求法,裂项求和以及放缩法的应用,也可以利用数学归纳法证明求解.

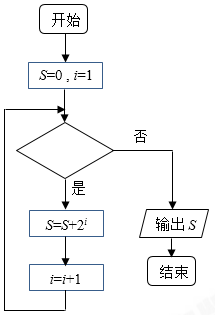
| A. | i≤4? | B. | i≤5? | C. | i≤6? | D. | i≤7? |
| A. | $\frac{1}{{{{({a_1}•{a_n})}^n}}}$ | B. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$ | C. | $\frac{1}{{{{({a_1}•{a_n})}^{n+1}}}}$ | D. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^{n+1}}}}$ |
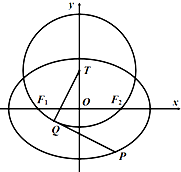 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.