题目内容
化简:cos8x-sin8x+
sin2xsin4x.
| 1 |
| 4 |
考点:三角函数的化简求值
专题:计算题,三角函数的求值
分析:利用同角三角函数的基本关系、二倍角公式、两角和差余弦公式化简,可得.
解答:
解:cos8x-sin8x+
sin2xsin4x=(cos4x-sin4x)(cos4x+sin4x)+
sin2xsin4x
=(cos2x-sin2x)(cos4x+sin4x)+
sin2xsin4x
=cos2x (1-2sin2xcos2x)+
sin2xsin4x
=cos2x (1-
sin22x )+
sin2xsin4x
=cos2x(1-
•
)+
sin2xsin4x
=cos2x-
+
sin2xsin4x
=
cos2x+
=
cos2x+
=cos2x.
| 1 |
| 4 |
| 1 |
| 4 |
=(cos2x-sin2x)(cos4x+sin4x)+
| 1 |
| 4 |
=cos2x (1-2sin2xcos2x)+
| 1 |
| 4 |
=cos2x (1-
| 1 |
| 2 |
| 1 |
| 4 |
=cos2x(1-
| 1 |
| 2 |
| 1-cos4x |
| 2 |
| 1 |
| 4 |
=cos2x-
| cos2x-cos2xcos4x |
| 4 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| cos2xcos4x+sin2xsin4x |
| 4 |
=
| 3 |
| 4 |
| cos(4x-2x) |
| 4 |
点评:本题主要考查同角三角函数的基本关系、二倍角公式、两角和差的余弦公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
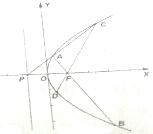 如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且
如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且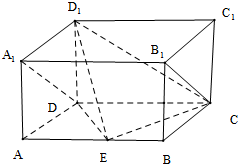 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.