题目内容
已知函数f(x)=
g(x)=
,则函数f[g(x)]的所有零点之和是( )
|
|
A、-
| ||||
B、
| ||||
C、-1+
| ||||
D、1+
|
考点:函数的零点
专题:计算题,函数的性质及应用
分析:先求得f[g(x)]的解析式,x≥0时,由2x2-2x-2-1=0,可解得:x=1+
或1-
(小于0,舍去);x<0时,由
+2=0,可解得:x=-
,从而可求函数f[g(x)]的所有零点之和.
| 3 |
| 3 |
| 1 |
| x |
| 1 |
| 2 |
解答:
解:∵f(x)=
g(x)=
,
∴f[g(x)]=
,且f[g(x)]=x2-2x+2,( 0<x<2)
∵x≥2或x=0时,由2x2-2x-2-1=0,可解得:x=1+
或1-
(小于0,舍去);
x<0时,由
+2=0,可解得:x=-
.
当 0<x<2时,由x2-2x+2=0,无解.
∴函数f[g(x)]的所有零点之和是1+
-
=
+
.
故选:B.
|
|
∴f[g(x)]=
|
∵x≥2或x=0时,由2x2-2x-2-1=0,可解得:x=1+
| 3 |
| 3 |
x<0时,由
| 1 |
| x |
| 1 |
| 2 |
当 0<x<2时,由x2-2x+2=0,无解.
∴函数f[g(x)]的所有零点之和是1+
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故选:B.
点评:本题主要考察了函数的零点,函数的性质及应用,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)的定义域为M,若函数f(x)满足条件[m,n]⊆M,使f(x)在[m,n]上的值域是[
,
],则成f(x)为“半缩函数”,若函数f(x)=log3(3x+λ)为“半缩函数”,则λ的范围是( )
| m |
| 2 |
| n |
| 2 |
| A、(0,1) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
已知△ABC不是直角三角形,三个角∠A、∠B、∠C对应的边分别是a、b、c,记ωA=
•
,ωB=
•
,ωC=
•
,下列结论中,错误的是( )
| AB |
| AC |
| BC |
| BA |
| CA |
| CB |
| A、ωA+ωB=c2 |
| B、ωAωBωC=-(abc)2 |
| C、若ωA=ωB=ωC,则△ABC为等边三角形 |
| D、ωAtanA=ωBtanB=ωCtanC |
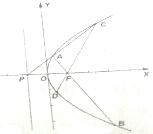 如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且
如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且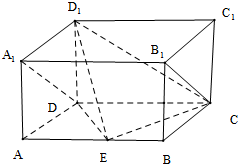 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.