题目内容
16.已知函数y=($\frac{1}{3}$)|x|.(1)作出函数的图象(简图);
(2)由图象指出其单调区间;
(3)由图象指出当x取什么值时有最值,并求出最值.
分析 先去绝对值,根据指数的图象和性质即可作出图象,找到单调区间和最值.
解答 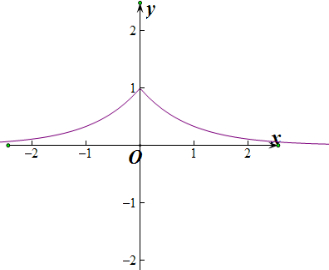 解:(1)y=($\frac{1}{3}$)|x|=$\left\{\begin{array}{l}{(\frac{1}{3})^{x},x≥0}\\{{3}^{x},x<0}\end{array}\right.$
解:(1)y=($\frac{1}{3}$)|x|=$\left\{\begin{array}{l}{(\frac{1}{3})^{x},x≥0}\\{{3}^{x},x<0}\end{array}\right.$
图象如图所示,
(2)由图象可知,函数在(-∞,0)上为增函数,在(0,+∞)上为减函数,
(3)由(2)可知,当x=0时,有最大值,最大值为1.
点评 本题考查了指数函数的图象和画法以及图象的识别,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一个几何体的三视图如图所示,这个几何体的全面积为( )


| A. | 12πcm2 | B. | 9πcm2 | C. | 6πcm2 | D. | 5πcm2 |
7.在三棱锥S-ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,SA=SC=2.AC的中点为M,∠SMB的余弦值为$\frac{\sqrt{3}}{3}$,若S、A、B、C都在同一球面上,则该球的表面积为( )
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
11.如果a<3,则下列结论一定正确的是( )
| A. | a2>9 | B. | a2<9 | C. | a3>27 | D. | a3<27 |
1.已知tanα=$\frac{4}{3}$,tan(α-β)=-$\frac{1}{3}$,则tanβ的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{9}{13}$ | D. | $\frac{13}{9}$ |
8.若函数f(x)=ax-lnx在区间(2,+∞)单调递增,则a的取值范围是( )
| A. | [$\frac{1}{2}$,+∞) | B. | (-∞,-1] | C. | (-∞,-2] | D. | [1,+∞) |
 如图所示,在三棱锥P-ABC中,E、F分别是PA、PC的中点,记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
如图所示,在三棱锥P-ABC中,E、F分别是PA、PC的中点,记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.