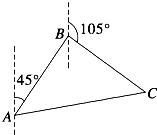题目内容
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c= ![]() ,且4sin2
,且4sin2 ![]() ﹣cos2C=
﹣cos2C= ![]()
(1)求角C的大小;
(2)求△ABC的面积.
【答案】
(1)解:∵A+B+C=180°,由 ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
整理得:4cos2C﹣4cosC+1=0,
解得: ![]() ,
,
由于:0<C<π,
可得:C= ![]() .
.
(2)解:∵由余弦定理可得:c2=a2+b2﹣2abcosC,即:7=a2+b2﹣ab,
∴7=(a+b)2﹣3ab,
∵由条件a+b=5,
∴可得:7=25﹣3ab,解得:ab=6,
∴ ![]() .
.
【解析】(1)由三角函数恒等变换的应用化简已知等式可得4cos2C﹣4cosC+1=0,可求 ![]() ,结合范围0<C<π,即可得解C的值.(2)由余弦定理可得7=(a+b)2﹣3ab,结合条件a+b=5,可求ab的值,进而利用三角形面积公式即可计算得解.
,结合范围0<C<π,即可得解C的值.(2)由余弦定理可得7=(a+b)2﹣3ab,结合条件a+b=5,可求ab的值,进而利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识,掌握余弦定理:![]() ;
;![]() ;
;![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
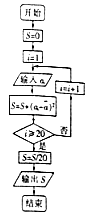
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值.