题目内容
【题目】已知数列{an}满足：a1=﹣13，a6+a8=﹣2，且an﹣1=2an﹣an+1（n≥2），则数列{ 
}的前13项和为（ ）
A.
B.﹣
C.
D.﹣
【答案】B
【解析】解：an﹣1=2an﹣an+1（n≥2）， 可得an+1﹣an=an﹣an﹣1 ，
可得数列{an}为等差数列，设公差为d，
由a1=﹣13，a6+a8=﹣2，即为2a1+12d=﹣2，
解得d=2，
则an=a1+（n﹣1）d=2n﹣15．
= 
= 
（ 
﹣ 
），
即有数列{ }的前13项和为 （ 
﹣ 
+ ﹣ 
+…+ 
﹣ 
）
= ×（﹣ ﹣ ）=﹣ ．
故选：B．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系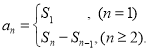
才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】对一批共50件的某电器进行分类检测，其重量（克）统计如下：
质量段 | [80，85） | [85，90） | [90，95） | [95，100] |
件数 | 5 | a | 15 | b |
规定重量在82克及以下的为“A”型，重量在85克及以上的为“B”型，已知该批电器有“A“型2件
（1）从该批电器中任选1件，求其为“B”型的概率；
（2）从重量在[80，85）的5件电器中，任选2件，求其中恰有1件为“A”型的概率．
