题目内容
【题目】设A、B分别为双曲线 ![]() 的左右顶点,双曲线的实轴长为4
的左右顶点,双曲线的实轴长为4 ![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为 ![]() .
.
(1)求双曲线的方程;
(2)已知直线 ![]() 与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使
与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使 ![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
【答案】
(1)解:由实轴长为 ![]() ,得
,得 ![]() ,
,
渐近线方程为 ![]() x,即bx﹣2
x,即bx﹣2 ![]() y=0,
y=0,
∵焦点到渐近线的距离为 ![]() ,
,
∴ ![]() ,又c2=b2+a2,∴b2=3,
,又c2=b2+a2,∴b2=3,
∴双曲线方程为: ![]()
(2)解:设M(x1,y1),N(x2,y2),D(x0,y0),则x1+x2=tx0,y1+y2=ty0,
由 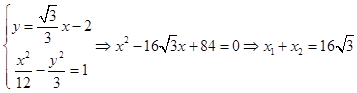 ,
,
∴y1+y2= ![]() ﹣4=12,
﹣4=12,
∴ 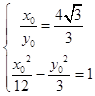 ,解得
,解得 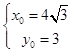 ,∴t=4,
,∴t=4,
∴ ![]() ,t=4
,t=4
【解析】(1)由实轴长可得a值,由焦点到渐近线的距离可得b,c的方程,再由a,b,c间的平方关系即可求得b;(2)设M(x1 , y1),N(x2 , y2),D(x0 , y0),则x1+x2=tx0 , y1+y2=ty0 , 则x1+x2=tx0 , y1+y2=ty0 , 联立直线方程与双曲线方程消掉y得x的二次方程,由韦达定理可得x1+x2 , 进而求得y1+y2 , 从而可得 ![]() ,再由点D在双曲线上得一方程,联立方程组即可求得D点坐标,从而求得t值;
,再由点D在双曲线上得一方程,联立方程组即可求得D点坐标,从而求得t值;

练习册系列答案
相关题目
