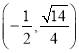题目内容
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)在(-∞,- ![]() )上单调递减,在(-
)上单调递减,在(-![]() ,
, ![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减;(2)实数m的取值范围为[1,+∞).
,+∞)上单调递减;(2)实数m的取值范围为[1,+∞).
【解析】试题分析:(Ⅰ)对函数进行求导得![]() ,分别解不等式
,分别解不等式![]() 和
和![]() 可得单调区间;(Ⅱ) 令
可得单调区间;(Ⅱ) 令![]() ,首先得到
,首先得到![]() ,对函数
,对函数![]() 进行二次求导,得到
进行二次求导,得到![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,对
,对![]() 分为
分为![]() 和
和![]() 两种情形,判断
两种情形,判断![]() 和0的关系,得到
和0的关系,得到![]() 的单调性,进而得到其与
的单调性,进而得到其与![]() 的关系,从而可得结论.
的关系,从而可得结论.
试题解析:(Ⅰ)由已知得![]() ,当
,当![]() ,即
,即![]() 时,
时, ![]() 或
或![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() ,所以f(x)在
,所以f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)令![]() ,
, ![]() ,
,
由已知可得![]() ,即
,即![]() ,下面只要考虑
,下面只要考虑![]() 的情况即可.
的情况即可.
g′(x)=(2-x2)ex-1-m,令h(x)=(2-x2)ex-1-m,则h′(x)=-(x2+2x-2)ex-1,
因为x≥1,所以x2+2x-2>0,所以h′(x)<0,
所以h(x)在[1,+∞)上单调递减,即g′(x)在[1,+∞)上单调递减,则g′(x)≤g′(1)=1-m.
①当1-m≤0,即m≥1时,此时g′(x)≤0,所以g(x)在[1,+∞)上单调递减,所以g(x)≤g(1)=0,满足条件;
②当1-m>0,即-1≤m<1时,此时g′(1)>0,g′(2)=-2e-m<0,所以存在x0∈(1,2),使得g′(x0)=0,则当1<x<x0时,g′(x)>0;
当x>x0时,g′(x)<0,所以g(x)在[1,x0]上单调递增,在(x0,+∞)上单调递减,
所以当x∈[1,x0]时,g(x)≥g(1)=0,此时不满足条件.
综上所述,实数m的取值范围为![]() .
.

练习册系列答案
相关题目