题目内容
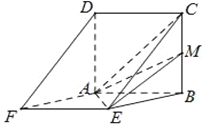
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.
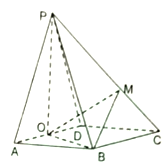
(Ⅰ)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,
, ![]() 为等边三角形,且
为等边三角形,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:⑴由![]() 得
得![]() ,底面为菱形,
,底面为菱形, ![]() ,利用面面垂直判定定理证明;
,利用面面垂直判定定理证明;
⑵法一:由面![]() 面
面![]() ,推出
,推出![]() ,计算出
,计算出![]() ,则
,则![]() ;法二:推出
;法二:推出![]() 面
面![]() ,
, ![]() ,先计算出
,先计算出![]() ,
, ![]() ,,然后
,,然后![]()
解析:(Ⅰ)∵PA=PD,AO=OD,∴PO⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,∴BO⊥AD,
PO∩BO=O,∴AD⊥平面POB
又AD平面PAD,∴平面POB⊥平面PAD;
(Ⅱ)方法一
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO⊥AD,
∴PO⊥平面ABCD,
∵![]() 平面ABCD
平面ABCD
∴PO⊥OB
∵![]() 为等边三角形,
为等边三角形, ![]() ,∴
,∴![]() ,
,
∵底面ABCD为菱形,∠BAD=60°,![]() ∴
∴![]()
∴![]()
由(Ⅰ) AD⊥平面POB∴BC⊥平面POB
∴![]()
方法二
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO⊥AD,
∴PO⊥平面ABCD,
∵![]() 为等边三角形,
为等边三角形, ![]() ,∴
,∴![]() ,
,
∵底面ABCD为菱形,∠BAD=60°,![]()
由(Ⅰ)BO⊥AD∴![]()
∵PM=2MC
∴![]()

【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
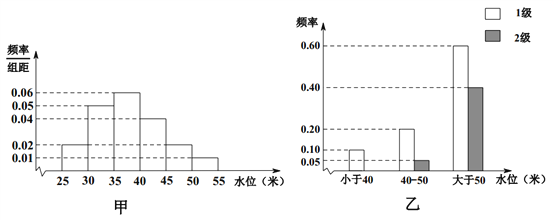
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.