题目内容
【题目】已知函数![]() .
.
(1)求证:函数![]() 有唯一零点;
有唯一零点;
(2)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)求出![]() ,先证明
,先证明![]() 在区间
在区间![]() 上为增函数,又
上为增函数,又![]() ,
,![]() ,所以
,所以![]() 在区间
在区间![]() 上恰有一个零点,而
上恰有一个零点,而![]() 在
在![]() 上恒成立,在
上恒成立,在![]() 上无零点,从而可得结果;(2))设
上无零点,从而可得结果;(2))设![]() 的零点为
的零点为![]() ,即
,即![]() . 原不等式可化为
. 原不等式可化为![]() ,令
,令![]() 若
若![]() ,可得
,可得![]() ,等式左负右正不相等,若
,等式左负右正不相等,若![]() ,等式左正右负不相等,只能
,等式左正右负不相等,只能![]() ,
,![]() ,即
,即![]() 求所求.
求所求.
试题解析:(1)![]() ,
,
易知![]() 在
在![]() 上为正,因此
上为正,因此![]() 在区间
在区间![]() 上为增函数,又
上为增函数,又![]() ,
,![]()
因此![]() ,即
,即![]() 在区间
在区间![]() 上恰有一个零点,
上恰有一个零点,
由题可知![]() 在
在![]() 上恒成立,即在
上恒成立,即在![]() 上无零点,
上无零点,
则![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
(2)设![]() 的零点为
的零点为![]() ,即
,即![]() . 原不等式可化为
. 原不等式可化为![]() ,
,
令![]() ,则
,则![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,故只求
上单调递增,故只求![]() ,,设
,,设![]() ,
,
下面分析![]() ,设
,设![]() ,则
,则![]() ,
,
可得![]() ,即
,即![]()
若![]() ,等式左负右正不相等,若
,等式左负右正不相等,若![]() ,等式左正右负不相等,只能
,等式左正右负不相等,只能![]() .
.
因此![]() ,即
,即![]() 求所求.
求所求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
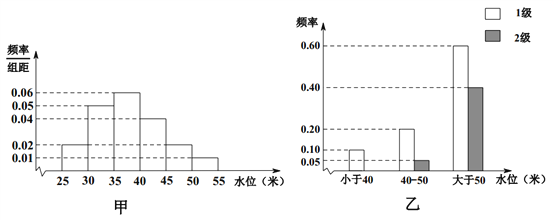
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
