题目内容
【题目】已知函数
，其中
.
（1）试讨论函数
的单调性及最值；
（2）若函数
不存在零点，求实数
的取值范围.
【答案】(1)见解析；（2）
【解析】试题分析：（1）讨论函数单调性，先明确函数定义域然后求导解不等式即可，当然要注意参数的讨论对导函数符号判断的影响；（2）函数
不存在零点，即函数的最大值恒小于零或者函数的最小值恒大于零，故先求出
的最值然后解不等式即可.
（Ⅰ）由
得：
⑴当
时, 
在
单调递增，
没有最大值，也没有最小值
⑵若
，
当
时, 
, 
在
单调递增
当
时， 
, 
在
单调递减，
所以当
时， 
取到最大值
没有最小值
（Ⅱ）
由
当
时, 
, 
单调递增，
当
时， 
, 
单调递减，
所以当
时 ， 
取到最大值
,
又
时， 有 
，
所以要使
没有零点，
只需
所以实数
的取值范围是： 
【题目】世界那么大，我想去看看，处在具有时尚文化代表的大学生们旅游动机强烈，旅游可支配收入日益增多，可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出（单位：百元）的情况，相关部门随机抽取了某大学的
名学生进行问卷调查，并把所得数据列成如下所示的频数分布表：
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
（Ⅰ）求所得样本的中位数（精确到百元）；
（Ⅱ）根据样本数据，可近似地认为学生的旅游费用支出
服从正态分布
，若该所大学共有学生
人，试估计有多少位同学旅游费用支出在
元以上；
（Ⅲ）已知样本数据中旅游费用支出在
范围内的
名学生中有
名女生， 
名男生，现想选其中
名学生回访，记选出的男生人数为
，求
的分布列与数学期望.
附：若
，则
，
， 
.
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图（甲）所示；依据当地的地质构造，得到水位与灾害等级的频率分布条形图如图（乙）所示．
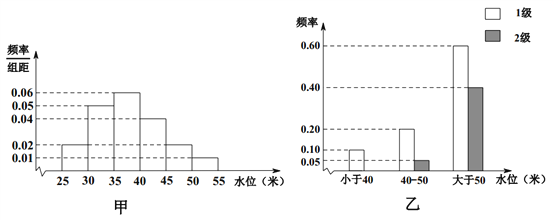
试估计该河流在8月份水位的中位数；
（1）以此频率作为概率，试估计该河流在8月份发生1级灾害的概率；
（2）该河流域某企业，在8月份，若没受1、2级灾害影响，利润为500万元；若受1级灾害影响，则亏损100万元；若受2级灾害影响则亏损1000万元．
现此企业有如下三种应对方案：
方案 | 防控等级 | 费用（单位：万元） |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问，如仅从利润考虑，该企业应选择这三种方案中的哪种方案？说明理由．
