题目内容
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点
,且过点![]() ,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
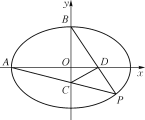
(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
【答案】(1)![]() +y2=1;(2)
+y2=1;(2)![]() -1
-1
【解析】
(1)由离心率![]() ,再把点
,再把点![]() 坐标代入
坐标代入![]() =1,结合
=1,结合![]() 可求得
可求得![]() ,得椭圆标准方程;
,得椭圆标准方程;
(2)设直线![]() 方程为
方程为![]() ,可求得
,可求得![]() 的坐标,由
的坐标,由![]() 共线求得
共线求得![]() 点坐标,这样可求得
点坐标,这样可求得![]() ,令
,令![]() 换元后用基本不等式求得最大值.
换元后用基本不等式求得最大值.
(1) 由题意得: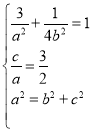 得a2=4,b2=1,
得a2=4,b2=1,
故椭圆C的标准方程为:![]() +y2=1.
+y2=1.
(2) 由题意设lAP:y=k(x+2),-![]() <k<0,所以C(0,2k),
<k<0,所以C(0,2k),
由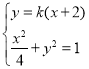 消y得(1+4k2)x2+16k2x+16k2-4=0,所以xAxP=
消y得(1+4k2)x2+16k2x+16k2-4=0,所以xAxP=![]() ,
,
由xA=-2得xP=![]() ,故yP=k(xP+2)=
,故yP=k(xP+2)=![]() ,
,
所以P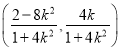 ,
,
设D(x0,0),因B(0,1),P,B,D三点共,所以kBD=kPB,故![]() =
=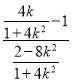 ,
,
解得x0=![]() ,得D
,得D![]() ,
,
所以S△PCD=SPAD-S△CAD=![]() ×AD×|yP-yC|
×AD×|yP-yC|
=![]() =
=![]() ,
,
因为-![]() <k<0,所以S△PCD=
<k<0,所以S△PCD=![]() =-2+2×
=-2+2×![]() ,
,
令t=1-2k,1<t<2,所以2k=1-t,
所以g(t)=-2+![]() =-2+
=-2+![]()
=-2+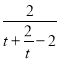 ≤-2+
≤-2+![]() =
=![]() -1,
-1,
当且仅当t=![]() 时取等号,此时k=
时取等号,此时k=![]() ,所以△PCD面积的最大值为
,所以△PCD面积的最大值为![]() -1.
-1.

练习册系列答案
相关题目