题目内容
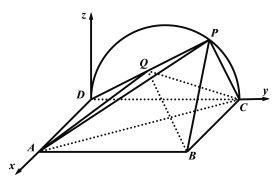
【题目】如图所示,已知矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
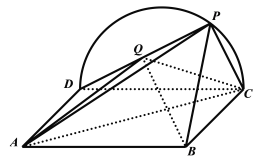
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,当三棱锥
,当三棱锥![]() 的体积最大且二面角
的体积最大且二面角![]() 的平面角的大小为
的平面角的大小为![]() 时,试确定
时,试确定![]() 的值.
的值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)由已知结合面面垂直性质定理,可证![]() 平面
平面![]() ,进而有
,进而有![]() ,再由
,再由![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点,且
的点,且![]() 为直径,得到
为直径,得到![]() ,可证明
,可证明
![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)当三棱锥![]() 的体积最大时,用等体积法,可得
的体积最大时,用等体积法,可得![]() 为
为![]() 的中点,建立空间直角坐标系,求出
的中点,建立空间直角坐标系,求出![]() 坐标,求出向量
坐标,求出向量![]() 坐标,由
坐标,由![]() ,求出向量
,求出向量![]() 坐标,分别求出平面
坐标,分别求出平面![]() 和平面
和平面![]() 的法向量,根据空间向量的面面角公式,得出关于
的法向量,根据空间向量的面面角公式,得出关于![]() 的方程,求解,即可得出结论.
的方程,求解,即可得出结论.
(1)由题设知:平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
∵![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,故
,故![]() .
.
又![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点,且
的点,且![]() 为直径,
为直径,
∴![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)如图所示,建立空间直角坐标系![]() ,
,
由等积法知![]() ,
,
当三棱锥![]() 的体积最大时,
的体积最大时,![]() 最大,
最大,
则![]() 到
到![]() 边的距离最大,此时
边的距离最大,此时![]() 为
为![]() 的中点.
的中点.
由题设知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由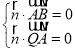 ,即
,即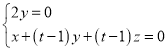 ,取
,取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由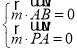 ,即
,即![]() ,取
,取![]() ,
,
因二面角![]() 的平面角的大小为
的平面角的大小为![]() ,
,
∴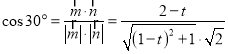 ,整理得
,整理得![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某教研部门对本地区甲、乙、丙三所学校高三年级进行教学质量抽样调查,甲、乙、丙三所学校高三年级班级数量(单位:个)如下表所示。研究人员用分层抽样的方法从这三所学校中共抽取6个班级进行调查.
学校 | 甲 | 乙 | 丙 |
数量 | 4 | 12 | 8 |
(1)求这6个班级中来自甲、乙、丙三所学校的数量;
(2)若在这6个班级中随机抽取2个班级做进一步调查,
①列举出所有可能的抽取结果;
②求这2个班级来自同一个学校的概率.