题目内容
【题目】设关于
的一元二次方程
．
（1）若
从
， 
， 
， 
四个数中任取的一个数， 
是从
， 
， 
三个数中任取的一个数，求上述方程有实根的概率；
（2）若
是从区间
上任取的一个数， 
是从区间
上任取的一个数，求上述方程有实根的概率．
【答案】（1）
；（2）
．
【解析】试题分析:(1)所有基本事件为从
， 
， 
， 
四个数中任取的一个数， 
是从
， 
， 
三个数中任取的一个数;所求事件为方程有实根
，即
,分别列举出
的组合,根据古典概型计算概率;(2)所有基本事件为
从区间
上任取的一个数， 
是从区间
上任取的一个数，所求事件为方程有实根, 即
,分别列出不等式画出区域,根据几何概型求出概率.
试题解析:
若方程
有实根，则
，即
．
（1）设“方程
有实根”为事件
，
∵
从
四个数中任取的一个数， 
是从
三个数中任取的一个数，
∴记
为所取两数的一个组合，则所有可能的取法有： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
共12种且每种均等可能被抽到，其中满足条件
的有
， 
， 
， 
， 
， 
， 
， 
， 
共9种，
∴
．
答：方程
有实根的概率为
．
（2）设“方程
有实根”为事件
，
∵
从区间
上任取的一个数， 
是从区间
上任取的一个数，
∴记
为所取两数的一个组合，则
， 
，
∴点
所在的区域为如图所示的矩形，
又条件
可化为
，即
，
∴满足条件
的点
所在的区域为如图所示的阴影部分区域
∴
．
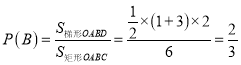答：方程
有实根的概率是
．
练习册系列答案
同步练习强化拓展系列答案
相关题目
