题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 时,不等式
时,不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .(2)
.(2)![]()
【解析】
试题分析:(1)当![]() 求导,可得
求导,可得![]() 的单调区间;(2)首先,要保证
的单调区间;(2)首先,要保证![]() 由意义,可得
由意义,可得![]() ;由题意得,不等式
;由题意得,不等式![]() 对于任意的
对于任意的![]() 恒成立,构造新函数
恒成立,构造新函数![]() ,
,![]() ,求导研究函数
,求导研究函数![]() 的性质,分情况讨论当
的性质,分情况讨论当![]() 时,不满足题意;当
时,不满足题意;当![]() 时,要使
时,要使![]() 时,不等式
时,不等式![]() 成立,需
成立,需![]() ,即
,即![]() ,此时要证
,此时要证![]() ,继续构造函数
,继续构造函数![]() ,求导可证得
,求导可证得![]() 在
在![]() 上单调递增,
上单调递增,![]() . 即
. 即![]() ,问题解决.
,问题解决.
试题解析:(1)当![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,,
时,,![]() 单调递减.
单调递减.
综上,![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .
.
(2) 由题意得,![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() .……①
.……①
由题意得,不等式![]() 对于任意的
对于任意的![]() 恒成立.
恒成立.
设![]() ,
,![]() .
.![]() .
.
当![]() 时,
时,![]() ,不满足题意;
,不满足题意;
当![]() 时,要使
时,要使![]() 时,不等式
时,不等式![]() 成立,
成立,
须![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,
,
设![]() ,
,![]() .
.
显然在![]() 上单调递增,所以
上单调递增,所以![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
即![]() . ……②
. ……②
由①②可知![]() 时,满足题意.
时,满足题意.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |

(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 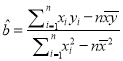 ,
, ![]() .
.
