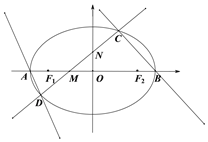
题目内容
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为![]() ,求△AOB面积的最大值,并求此时直线l的方程.
,求△AOB面积的最大值,并求此时直线l的方程.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)由离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() 可得
可得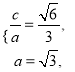 从而求得
从而求得![]() 的值,进而可得求椭圆
的值,进而可得求椭圆![]() 的方程;(2)直线
的方程;(2)直线![]() 的方程为
的方程为![]() ,由点到直线距离公式可得
,由点到直线距离公式可得![]() 与椭圆方程联立可得
与椭圆方程联立可得![]() ,再根据弦长公式可得
,再根据弦长公式可得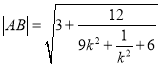 ,从而可得
,从而可得![]() ,进而可得△
,进而可得△![]() 面积的最大值.
面积的最大值.
试题解析:(1)设椭圆的半焦距为![]() ,依题意
,依题意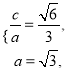 ∴
∴![]() ,
,
∴所求椭圆方程为![]() .
.
(2)设![]() ,
, ![]() ,
,
①当![]() ⊥
⊥![]() 轴时,
轴时, ![]() 为
为![]() ,代入
,代入![]() ,得
,得![]() ,∴
,∴![]() ;
;
②当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
由已知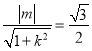 ,得
,得![]() ,
,
把![]() 代入椭圆方程,整理
代入椭圆方程,整理![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
∴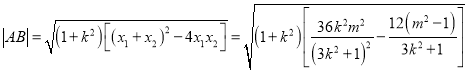
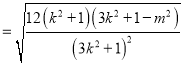
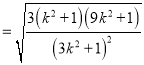
![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时,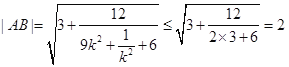 ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
综上所述![]() .
.
∴当![]() 最大时,△
最大时,△![]() 面积取最大值
面积取最大值![]() .
.

练习册系列答案
相关题目
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 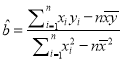 ,
, ![]() .
.