题目内容
【题目】已知函数f（x）=lg（1+x）+lg（1﹣x）．
（1）求函数f（x）的定义域；
（2）判断函数f（x）的奇偶性；
（3）求函数f（x）的值域．
【答案】
（1）解：由 
，求得﹣1＜x＜1，
∴函数f（x）的定义域为（﹣1，1）
（2）解：定义域关于原点对称，对于任意的x∈（﹣1，1），
∵f（﹣x）=lg（1﹣x）+lg（1+x）=f（x），∴f（x）为偶函数
（3）解：f（x）=lg[（1+x）（1﹣x）]=lg（1﹣x2）．
∵t=1﹣x2 ≤1，∴y≤lg1=0，
∴函数f（x）的值域为（﹣∞，0]
【解析】（1）由 ，求得函数f（x）的定义域．（2）根据定义域关于原点对称，再根据f（﹣x）=f（x），可得f（x）为偶函数．（3）化简f（x）为lg（1﹣x2），再根据t=1﹣x2 ≤1，求得f（x）≤lg1=0，由此求得函数f（x）的值域．
练习册系列答案
相关题目
【题目】已知某蔬菜商店买进的土豆
（吨）与出售天数
（天）之间的关系如表所示：
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）请根据表中数据在所给网格中绘制散点图；
（Ⅱ）请根据表中提供的数据，用最小二乘法求出
关于
的线性回归方程
（其中
保留2位有效数字）；
（Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
附：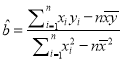 
， 
．
