题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
(I)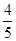 ,
,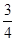 ;(II)(i)分布列见解析,
;(II)(i)分布列见解析,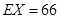 ;(ii)
;(ii)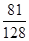 .
.
解析试题分析:(I)用指标大于或等于82所对应的的元件的个数除以总的元件个数即是正品的概率;(II)(i)根据题意分别求出一件A正品和一件B正品,一件A次品和一件B正品,一件A正品和一件B次品,一件A次品和一件B次品的概率,列出分布列,由公式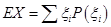 求出数学期望;(ii)根据题意设出5件元件中正品和次品的数量,列不等式
求出数学期望;(ii)根据题意设出5件元件中正品和次品的数量,列不等式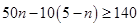 求解,根据解得的
求解,根据解得的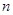 的值求解概率.
的值求解概率.
试题解析:(I)元件 为正品的概率约为
为正品的概率约为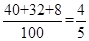 . 1分
. 1分
元件 为正品的概率约为
为正品的概率约为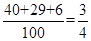 . 2分
. 2分
(II)(i)随机变量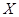 的所有取值为
的所有取值为 . 3分
. 3分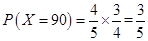 ;
; 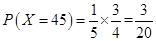 ;
;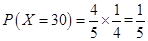 ;
; 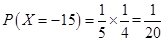 . 7分
. 7分
所以,随机变量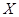 的分布列为:
的分布列为:
8分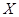
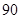
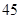
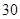
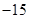
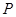
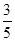
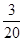
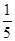
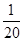
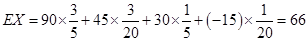 . 9分
. 9分
(ii)设生产的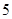 件元件
件元件 中正品有
中正品有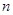 件,则次品有
件,则次品有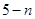 件.
件.
依题意,得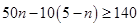 , 解得
, 解得 .
.
∴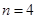 或
或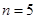 . 10分
. 10分
设“生产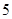 件元件
件元件 所获得的利润不少于
所获得的利润不少于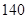 元”为事件
元”为事件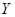 ,
,
则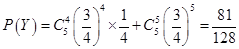 . 12分
. 12分
考点:1、随机事件的概率;2、求离散型随机变量的分布列和数学期望;3、解不等式.

 阅读快车系列答案
阅读快车系列答案某食品企业一个月内被消费者投诉的次数用 表示,椐统计,随机变量
表示,椐统计,随机变量 的概率分布如下:
的概率分布如下:
 | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 2a | a |
 的数学期望;
的数学期望;(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
某种产品按质量标准分为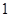 ,
, ,
,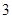 ,
,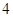 ,
,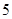 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
| 等级 | 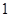 |  | 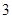 | 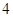 | 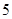 |
| 频率 | 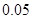 | 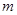 | 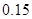 | 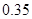 | 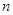 |
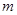 ,
,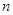 ;
;(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.
某品牌汽车的4 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4 店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用
店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用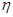 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.
| 付款方式 | 一次 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
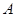 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率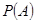 ;
;(2)求
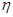 的分布列及其数学期望
的分布列及其数学期望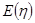 .
. 为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”
(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?
(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下(人数) | 120分以上(人数) | 合计(人数) |
| 一班 | | | |
| 二班 | | | |
| 合计 | | | |
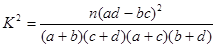 ,其中
,其中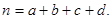
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
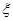 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求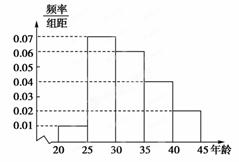
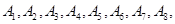 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为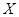 .若
.若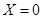 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.


 •
•