题目内容
小波以游戏方式决定参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从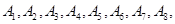 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为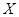 .若
.若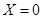 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.
(I)求小波参加学校合唱团的概率;
(II)求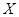 的分布列和数学期望.
的分布列和数学期望.
(I)小波参加学校合唱团的概率为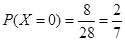 .
.
(II)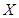 的分布列为:
的分布列为: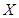
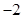
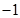
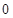
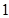
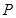
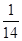
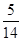
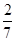
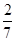
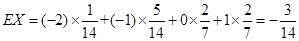 .
.
解析试题分析:(I)观察图形,确定从8个点中任意取两点为向量终点的方法数;
计算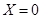 时,两向量夹角为直角的情况数;
时,两向量夹角为直角的情况数;
应用古典概型概率的计算公式计算“小波参加学校合唱团的概率”.
(II)注意到两向量数量积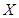 的所有可能取值为
的所有可能取值为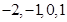
分别计算相应概率,写出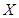 的分布列.关键是计算概率要准确.
的分布列.关键是计算概率要准确.
利用数学期望计算公式得到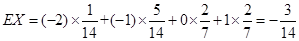 .
.
本题难度不大,突出了对古典概型概率的计算方法,以及数学期望的计算公式等所学知识的考查.
试题解析:(I)从8个点中任意取两点为向量终点的不同取法共有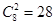 种,
种,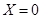 时,两向量夹角为直角共有8种情形;所以小波参加学校合唱团的概率为
时,两向量夹角为直角共有8种情形;所以小波参加学校合唱团的概率为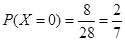 . 4分
. 4分
(II)两向量数量积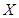 的所有可能取值为
的所有可能取值为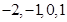
当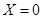 时,
时,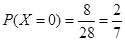
当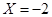 时,有2种情形
时,有2种情形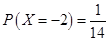
当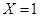 时,有8种情形
时,有8种情形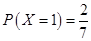
当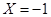 时,有10种情形
时,有10种情形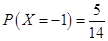 . 8分
. 8分
所以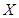 的分布列为:
的分布列为:
10分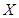
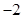
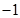
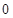
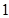
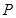
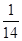
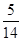
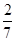
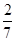
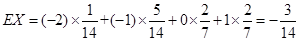 . 12分
. 12分
考点:古典概型概率的计算,离散性随机变量的分布列、期望.

某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 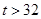 ℃ ℃ |
| 天数 | 6 | 12 | 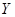 | 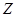 |
某水果商根据多年的销售经验,六月份的日最高气温t (单位:℃)对西瓜的销售影响如下表:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 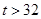 ℃ ℃ |
日销售额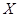 (千元) (千元) | 2 | 5 | 6 | 8 |
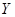 ,
, 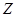 的值;
的值;(Ⅱ) 若视频率为概率,求六月份西瓜日销售额的期望和方差;
(Ⅲ) 在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
(2)当产品中的微量元素x,y满足x≥175且y≥75,该产品为优等品,
①用上述样本数据估计乙厂生产的优等品的数量;
②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
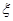 的分布列及其期望.
的分布列及其期望. 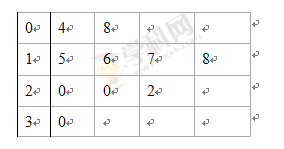
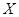 ,求随机变量
,求随机变量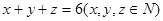 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;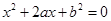 .
.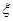 的分布列和数学期望.
的分布列和数学期望.