题目内容
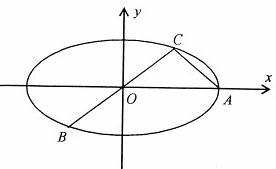
在平面直角坐标系中,已知△ABC的两个顶点B(-3,0),C(3,0)且三边AC、BC、AB的长成等差数列,求点A的轨迹方程.
∵B(-3,0)、C(3,0),△ABC的三边AC、BC、AB的长成等差数列,
∴|AC|+|AB|=2|BC|=12>|BC|,
根据椭圆的定义,可得顶点A的轨迹是以B、C为焦点,长轴长等于12的椭圆(长轴端点除外).
∵2a=12,2c=12,
∴a=6,c=3,可得b2=a2-c2=27.
因此,顶点A的轨迹方程为
+
=1(x≠±6).
∴|AC|+|AB|=2|BC|=12>|BC|,
根据椭圆的定义,可得顶点A的轨迹是以B、C为焦点,长轴长等于12的椭圆(长轴端点除外).
∵2a=12,2c=12,
∴a=6,c=3,可得b2=a2-c2=27.
因此,顶点A的轨迹方程为
| x2 |
| 36 |
| y2 |
| 27 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的直角顶点
的直角顶点 为动点,
为动点,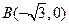 ,
,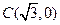 为两个定点,作
为两个定点,作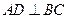 于
于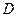 ,动点
,动点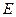 满足
满足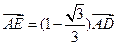 ,当点
,当点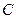 ,曲线
,曲线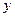 轴正半轴的交点为
轴正半轴的交点为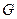 .(Ⅰ) 求曲线
.(Ⅰ) 求曲线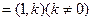 的直线
的直线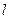 ,与曲线
,与曲线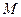 ,
,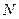 两点,使
两点,使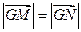 ,且
,且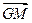 与
与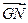 的夹角为
的夹角为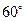 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.