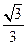题目内容
椭圆ax2+by2=1与直线x+y-1=0相交于A,B两点,C是AB的中点,若|AB|=2
,OC的斜率为
,求椭圆的方程.
| 2 |
| ||
| 2 |
设A(x1,y1),B(x2,y2),那么A、B的坐标是方程组
的解.
即:a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0,
因为
=-1,
所以
=
,
即
=
,
=
=
,所以b=
a①
再由方程组消去y得(a+b)x2-2bx+b-1=0,
由|AB|=
=
=
=2
,
得(x1+x2)2-4x1x2=4,即(
)2-4•
=4.②
由①②解得a=
,b=
,
故所求的椭圆的方程为
+
=1.
|
即:a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0,
因为
| y1-y2 |
| x1-x2 |
所以
| y1+y2 |
| x1+x2 |
| a |
| b |
即
| 2yc |
| 2xc |
| a |
| b |
| yc |
| xc |
| a |
| b |
| ||
| 2 |
| 2 |
再由方程组消去y得(a+b)x2-2bx+b-1=0,
由|AB|=
| (x1-x2)2+(y1-y2)2 |
| 2(x1-x2)2 |
| 2[(x1+x2)2-4x1x2] |
| 2 |
得(x1+x2)2-4x1x2=4,即(
| 2b |
| a+b |
| b-1 |
| a+b |
由①②解得a=
| 1 |
| 3 |
| ||
| 3 |
故所求的椭圆的方程为
| x2 |
| 3 |
| ||
| 3 |

练习册系列答案
相关题目
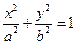 (
(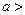
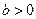 )的左、右焦点分别是
)的左、右焦点分别是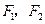 ,过
,过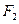 作倾斜角为
作倾斜角为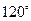 的直线与椭圆的一个交点为
的直线与椭圆的一个交点为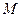 ,若
,若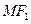 垂直于
垂直于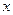 轴,则椭圆的离心率为( )
轴,则椭圆的离心率为( )