题目内容
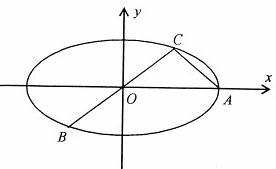
如图：已知椭圆A，B，C是长轴长为4的椭圆上三点，点A是长轴的一个端点，BC过椭圆的中心O，且
•
=0，|
|=2|
|．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）如果椭圆上两点P，Q使得直线CP，CQ与x轴围成底边在x轴上的等腰三角形，是否总存在实数λ使
=λ
？请给出证明．
| AC |
| BC |
| BC |
| AC |
（Ⅰ）求椭圆的标准方程；
（Ⅱ）如果椭圆上两点P，Q使得直线CP，CQ与x轴围成底边在x轴上的等腰三角形，是否总存在实数λ使
| PQ |
| AB |
（Ⅰ）设椭圆方程为
+
=1(a＞b＞0)，
∵椭圆的长轴长为4，
∴a=2，
∵点A是长轴的一个顶点，
∴A（2，0），
∵
•
=0，|
|=2|
|．
∴△AOC是等腰直角三角形，从而C（1，1），
代入椭圆方程得
+
=1⇒b2=
，
∴椭圆方程为
+
=1．
（Ⅱ）设直线lPC：y=kx+1-k（k≠0）
与椭圆方程
+
=1联立得到（3k2+1）x2+6k（1-k）x+3（1-k）2-4=0
则△=[6k（1-k）]2-4（3k2+1）[3（k-1）2-4]=4（3k+1）2＞0从而k≠-
且k≠0
设点P（x1，y1），而C（1，1），由韦达定理知1+x1=
⇒x1=
代回lPC：y=kx+1-k得到y1=
∵直线CP、CQ与x轴围成底边在x轴上的等腰三角形
∴直线CP、CQ的斜率互为相反数，即k≠-
，k≠
且k≠0
故设点Q（x2，y2），同理可知x2=
，y2=
所以
=(
，
)
∵椭圆是中心对称图形
∴B（-1，-1），
=(-3，-1)
故
=-
，即总存在实数λ使
=λ
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的长轴长为4，
∴a=2，
∵点A是长轴的一个顶点，
∴A（2，0），
∵
| AC |
| BC |
| BC |
| AC |
∴△AOC是等腰直角三角形，从而C（1，1），
代入椭圆方程得
| 1 |
| 4 |
| 1 |
| b2 |
| 4 |
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| 3y2 |
| 4 |
（Ⅱ）设直线lPC：y=kx+1-k（k≠0）
与椭圆方程
| x2 |
| 4 |
| 3y2 |
| 4 |
则△=[6k（1-k）]2-4（3k2+1）[3（k-1）2-4]=4（3k+1）2＞0从而k≠-
| 1 |
| 3 |
设点P（x1，y1），而C（1，1），由韦达定理知1+x1=
| 6k(k-1) |
| 3k2+1 |
| 3k2-6k-1 |
| 3k2+1 |
代回lPC：y=kx+1-k得到y1=
| -3k2-2k+1 |
| 3k2+1 |
∵直线CP、CQ与x轴围成底边在x轴上的等腰三角形
∴直线CP、CQ的斜率互为相反数，即k≠-
| 1 |
| 3 |
| 1 |
| 3 |
故设点Q（x2，y2），同理可知x2=
| 3k2+6k-1 |
| 3k2+1 |
| -3k2+2k+1 |
| 3k2+1 |
所以
| PQ |
| 12k |
| 3k2+1 |
| 4k |
| 3k2+1 |
∵椭圆是中心对称图形
∴B（-1，-1），
| AB |
故
| PQ |
| 4k |
| 3k2+1 |
| AB |
| PQ |
| AB |
练习册系列答案
相关题目
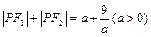，则点P的轨迹是（ ）。