题目内容
7.已知向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow b|=3$,$\overrightarrow a$在$\overrightarrow b$方向上的投影是$\frac{3}{2}$,则$\overrightarrow a•\overrightarrow b$=$\frac{9}{2}$.分析 $\overrightarrow a$在$\overrightarrow b$方向上的投影即|$\overrightarrow a$|cos<$\overrightarrow a$,$\overrightarrow b$>,利用平面向量数量积的定义计算即可.
解答 解:∵$\overrightarrow a$在$\overrightarrow b$方向上的投影是$\frac{3}{2}$,
∴|$\overrightarrow a$|cos<$\overrightarrow a$,$\overrightarrow b$>=$\frac{3}{2}$,
∴$\overrightarrow a•\overrightarrow b$=|$\overrightarrow a$||$\overrightarrow b$|cos<$\overrightarrow a$,$\overrightarrow b$>=$\frac{3}{2}$•3=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题考查平面向量数量积的几何意义,注意解题方法的积累,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.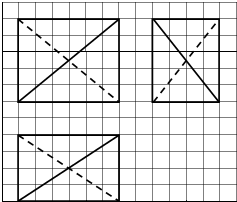 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |
2.已知定义在R上的函数f(x)的导函数为f′(x),满足f′(x)<f(x),f(2)=-2,f(1+x)=-f(1-x),则不等式f(x)<2ex的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
12.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点(x0,y0)使x0+ay0+2≤0成立,则实数a的取值范围是( )
| A. | a>1 | B. | a>-1 | C. | a≤1 | D. | a≤-1 |
19.下列四个函数中,既是奇函数又是定义域上的单调递增的是( )
| A. | y=2-x | B. | y=tanx | C. | y=x3 | D. | y=log3x |
 已知E、F是x轴上的点,坐标原点O为线段EF的中点,|$\overrightarrow{FG}|=10,|\overrightarrow{EF}$|=6,G,P是坐标平面上的动点,点P在线段FG上,EG的中点为H,且$\overrightarrow{PH}•\overrightarrow{EG}$=0.
已知E、F是x轴上的点,坐标原点O为线段EF的中点,|$\overrightarrow{FG}|=10,|\overrightarrow{EF}$|=6,G,P是坐标平面上的动点,点P在线段FG上,EG的中点为H,且$\overrightarrow{PH}•\overrightarrow{EG}$=0.