题目内容
15.以抛物线y=$\frac{1}{4}$x2的焦点为圆心,以焦点到准线的距离为半径的圆被双曲线$\frac{x^2}{4}$-y2=1的渐近线截得的弦长为$\frac{8\sqrt{5}}{5}$.分析 由抛物线方程求出抛物线的焦点坐标,得到圆心坐标和半径,由双曲线方程求出其渐近线方程,再由点到直线距离求得圆心到渐近线的距离,利用勾股定理求得弦长.
解答 解:由y=$\frac{1}{4}$x2,得x2=4y,∴F(0,1),则所求圆的方程为x2+(y-1)2=4,
由双曲线$\frac{x^2}{4}$-y2=1,得其渐近线方程为y=$±\frac{1}{2}x$,
不妨取y=$\frac{1}{2}x$,即x-2y=0,
则F(0,1)到直线x-2y=0的距离为d=$\frac{|-2|}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$,
∴弦长为$2\sqrt{4-(\frac{2\sqrt{5}}{5})^{2}}=\frac{8\sqrt{5}}{5}$.
故答案为:$\frac{8}{5}\sqrt{5}$.
点评 本题考查抛物线和双曲线的简单性质,考查了点到直线的距离公式,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.知a1=1,an+1=$\frac{a_n}{{3{a_n}+1}}$,则数列{an}的通项为an=( )
| A. | $\frac{1}{2n-1}$ | B. | 2n-1 | C. | $\frac{1}{3n-2}$ | D. | 3n-2 |
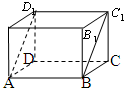 如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.
如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114. 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合). 如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.
如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.