��Ŀ����
14�� ��֪E��F��x���ϵĵ㣬����ԭ��OΪ�߶�EF���е㣬|$\overrightarrow{FG}|=10��|\overrightarrow{EF}$|=6��G��P������ƽ���ϵĶ��㣬��P���߶�FG�ϣ�EG���е�ΪH����$\overrightarrow{PH}•\overrightarrow{EG}$=0��
��֪E��F��x���ϵĵ㣬����ԭ��OΪ�߶�EF���е㣬|$\overrightarrow{FG}|=10��|\overrightarrow{EF}$|=6��G��P������ƽ���ϵĶ��㣬��P���߶�FG�ϣ�EG���е�ΪH����$\overrightarrow{PH}•\overrightarrow{EG}$=0��������P�Ĺ켣C�ķ��̣�
������ֱ֪��l����E��-3��0������켣C����A��B���㣬MΪAB���е㣬���OEM��������ֵ��
���� ����ȡEG���е�ΪH��˵��PH���߶�EG�Ĵ�ֱƽ���ߣ��õ�PE|=|PG|���ж�P��Ĺ켣Ϊ��Բ������켣����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$����⼴�ɣ�
�����Ƴ�A��B��E���㹲�ߣ���AB����ֱ�߷���Ϊx=my-3������Բ��������������Τ�ﶨ�����M����������ʾ�������ε�����ı���ʽ�����û�������ʽ����OEM��������
��� �⣺����ȡEG���е�ΪH����$\overrightarrow{PE}+\frac{1}{2}\overrightarrow{EG}=\overrightarrow{PH}$����$��\overrightarrow{PE}+\frac{1}{2}\overrightarrow{EG}��•\overrightarrow{EG}=0$����$\overrightarrow{PH}•\overrightarrow{EG}=0$��
��PH��GE����PH���߶�EG�Ĵ�ֱƽ���ߣ�����2�֣�
��|PE|=|PG|����|PE|+|PF|=|GF|=10��
��P��Ĺ켣Ϊ��Բ������켣����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$������4�֣�
��2a=10��a=5��2c=6��c=3��b2=a2-c2=16��
��$\frac{x^2}{25}+\frac{y^2}{16}=1$������6�֣�
����$\overrightarrow{OE}=��\overrightarrow{OA}+��1-����\overrightarrow{OB}=��\overrightarrow{OA}+\overrightarrow{OB}-��\overrightarrow{OB}$����$\overrightarrow{OE}-\overrightarrow{OB}=����\overrightarrow{OA}-\overrightarrow{OB}��$����$\overrightarrow{BE}=��\overrightarrow{BA}$��
��A��B��E���㹲�ߣ�����8�֣���
��E��-3��0����
��AB����ֱ�߷���Ϊx=my-3��
����$\left\{\begin{array}{l}x=my-3\\ \frac{x^2}{25}+\frac{y^2}{16}=1\end{array}\right.$�������ã�16m2+25��y2-96my-256=0��
��${y_1}+{y_2}=\frac{96m}{{16{m^2}+25}}$��
��M���������Ϊ${y_M}=\frac{{{y_1}+{y_2}}}{2}$=$\frac{48m}{{16{m^2}+25}}$������11�֣�
��${S_{��OEM}}=\frac{1}{2}|{\overrightarrow{OE}}||{y_M}|=\frac{1}{2}��3��$$\frac{48|m|}{{16{m^2}+25}}$=$\frac{72|m|}{{16{m^2}+25}}=\frac{72}{{16|m|+\frac{25}{|m|}}}��\frac{9}{5}$��
�൱$16|m|=\frac{25}{|m|}$����$m=��\frac{5}{4}$ʱ����OEM��������Ϊ$\frac{9}{5}$������13�֣�
���� ���⿼��ֱ������Բ���̵��ۺ�Ӧ�ã��켣���̵�����������ʽ��Ӧ�ã����������������������������麯���뷽�̵�˼���Ӧ�ã�

 ��ͼ����֪������Ϊ$\frac{\sqrt{3}}{2}$����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������M��2��1����OΪ����ԭ�㣬ƽ����OM��ֱ��l����ԲC�ڲ�ͬ������A��B��
��ͼ����֪������Ϊ$\frac{\sqrt{3}}{2}$����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������M��2��1����OΪ����ԭ�㣬ƽ����OM��ֱ��l����ԲC�ڲ�ͬ������A��B��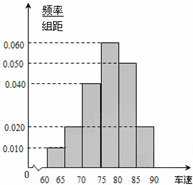 2014�ꡰ��һ���ڼ䣬���ٹ�·�����϶࣮ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�km/t���ֳ����Σ�[60��65����[65��70����[70��75����[75��80����[80��85����[85��90����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
2014�ꡰ��һ���ڼ䣬���ٹ�·�����϶࣮ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�km/t���ֳ����Σ�[60��65����[65��70����[70��75����[75��80����[80��85����[85��90����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��