题目内容
17.已知函数f(x)=$\frac{|x+1|-|x-1|}{2}$,函数g(x)=ax2-2x+1.若函数y=f(x)-g(x)恰好有2个不同的零点,则实数a的取值范围为(-∞,0)∪(0,$\frac{9}{4}$).分析 化函数y=f(x)-g(x)恰好有2个不同零点为函数f(x)+2x-1与函数y=ax2的图象有两个不同的交点,从而解得.
解答 解:∵f(x)-(ax2-2x+1)=0,
∴f(x)+2x-1=ax2,
而f(x)+2x-1=$\left\{\begin{array}{l}{2x-2,x<-1}\\{3x-1,-1≤x≤1}\\{2x,x>1}\end{array}\right.$,
作函数y=f(x)+2x-1与函数y=ax2的图象如下,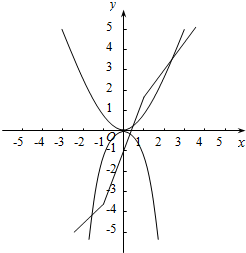
①当a<0时,恒有两个焦点;
②当a=0时,不满足题意;
③当a>0时,当有y=ax2与y=3x-1相切,此时a为临界值,联立得到:
ax2-3x+1=0,△=9-4a=0,a=$\frac{9}{4}$,此时图象如下图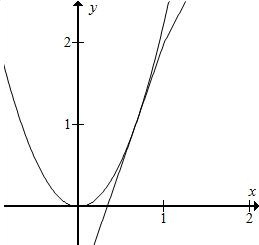
所以0<a<$\frac{9}{4}$;
综上a的取值范围是:(-∞,0)∪(0,$\frac{9}{4}$).
点评 本题考查了数形结合的思想应用及函数的零点与函数的图象的关系应用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
7.已知集合A={x|-5<x<5},B={x|0<x≤7}.则A∪B=( )
| A. | (0,5) | B. | (-5,7) | C. | (-5,7] | D. | [-5,7) |
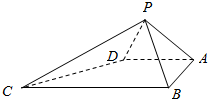 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.