题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+5x+4(x≤0)}\\{2|x-2|(x>0)}\end{array}\right.$,若函数y=f(x)-a|x|恰有3个零点,则a的取值范围是a=0或a≥2.分析 由y=f(x)-a|x|=0得f(x)=a|x|,利用数形结合即可得到结论.
解答  解:由y=f(x)-a|x|=0得f(x)=a|x|,
解:由y=f(x)-a|x|=0得f(x)=a|x|,
作出函数y=f(x),y=a|x|的图象.
当a=0,满足条件,
当a≥2时,此时y=a|x|与f(x)有三个交点,
故答案为:a=0或a≥2.
点评 本题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
15.已知Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | $\frac{5}{2}$ | B. | 5 | C. | 7 | D. | 9 |
19.如图所示是某一几何体的三视图,则这个几何体是( )
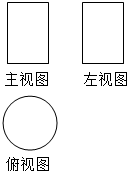

| A. | 圆柱体 | B. | 圆锥体 | C. | 正方体 | D. | 球体 |