题目内容
8.在平面直角坐标系xOy中,圆x2+y2=16的切线与x轴、y轴的正半轴分别交于A、B两点,则△AOB面积的最小值为16.分析 用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得ab=4$\sqrt{{a}^{2}+{b}^{2}}$≤$\frac{1}{2}$(a2+b2),令t=$\sqrt{{a}^{2}+{b}^{2}}$,可得t的最小值为8,进而得到答案.
解答 解:设切线方程为bx+ay-ab=0(a>0,b>0),
由圆心到直线的距离等于半径得$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=4,
所以ab=4$\sqrt{{a}^{2}+{b}^{2}}$≤$\frac{1}{2}$(a2+b2),令t=$\sqrt{{a}^{2}+{b}^{2}}$,
则有t2-8t≥0,t≥8,故t的最小值为8.
∴t=|AB|的最小值为8,
∴△AOB面积的最小值为$\frac{1}{2}×4×8$=16.
故答案为:16.
点评 本题考查点到直线的距离公式和基本不等式的应用,体现了换元的思想(在换元时应该注意等价换元).

练习册系列答案
相关题目
19.已知倾斜角为α的直线l与直线x+2y-3=0垂直,则cos($\frac{2015π}{2}$-2α)的值为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 2 | D. | -$\frac{1}{2}$ |
20.函数y=f(x)的定义域是(-1,1),则函数f(2x-1)的定义域为( )
| A. | (0,1) | B. | (-1,1) | C. | (-3,1) | D. | (-1,0) |
18.已知定义在R上的函数f(x)=$\left\{\begin{array}{l}{x^2}+2,x∈[0,1)\\ 2-{x^2},x∈[-1,0)\end{array}$且f(x+2)=f(x).若方程f(x)-kx-2=0有三个不相等的实数根,则实数k的取值范围是( )
| A. | $(\frac{1}{3},1)$ | B. | $(-\frac{1}{3},-\frac{1}{4})$ | C. | $(\frac{1}{3},1)∪(-1,-\frac{1}{3})$ | D. | $(-\frac{1}{3},-\frac{1}{4})∪(\frac{1}{4},\frac{1}{3})$ |
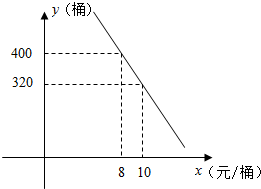 高一某班共有学生43人,据统计原来每人每年用于购买饮料的平均支出是120元.若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用260元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图直线所示关系.
高一某班共有学生43人,据统计原来每人每年用于购买饮料的平均支出是120元.若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用260元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图直线所示关系.