题目内容
(本小题满分14分)已知函数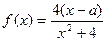 .
.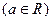 (Ⅰ)判断
(Ⅰ)判断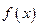 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程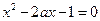 的两实根为
的两实根为 ,证明函数
,证明函数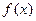 是
是 上的增函数.
上的增函数.
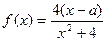 .
.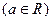 (Ⅰ)判断
(Ⅰ)判断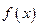 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程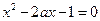 的两实根为
的两实根为 ,证明函数
,证明函数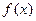 是
是 上的增函数.
上的增函数.(1)既不是奇函数,也不是偶函数 (2)略
:(Ⅰ)当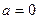 时,
时,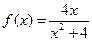 , 对任意
, 对任意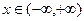 ,
,
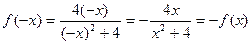 ,
, 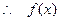 为奇函数. …2分
为奇函数. …2分
当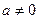 时,
时,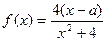 , 取
, 取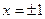 ,得
,得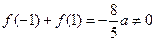 ,
,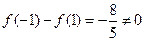 ,
,
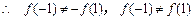 ,
, 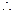 函数
函数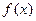 既不是奇函数,也不是偶函数.5分
既不是奇函数,也不是偶函数.5分
(Ⅱ)法一:证明: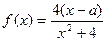 ,任取
,任取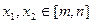 且
且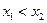 ,………6分
,………6分
则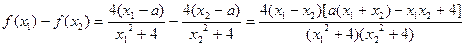 ………7分
………7分
设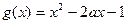 ,则
,则 即
即 ,…9分
,…9分
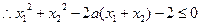 ,又
,又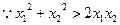 ………11分
………11分
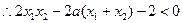 ,即
,即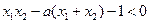 ………12分
………12分
又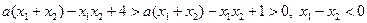 ,
,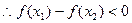 …13分
…13分
即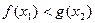 ,故
,故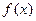 在区间
在区间 上是增函数. ………14分
上是增函数. ………14分
法二:证明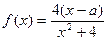 ,
, ……7分
……7分
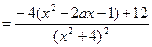 设
设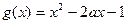 ,当
,当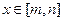 时,
时, 即
即

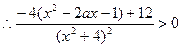 13分故
13分故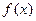 在区间
在区间 上是增函数.
上是增函数.
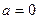 时,
时,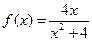 , 对任意
, 对任意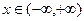 ,
,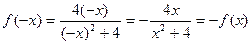 ,
, 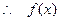 为奇函数. …2分
为奇函数. …2分 当
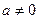 时,
时,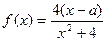 , 取
, 取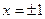 ,得
,得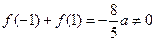 ,
,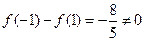 ,
, 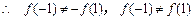 ,
, 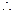 函数
函数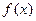 既不是奇函数,也不是偶函数.5分
既不是奇函数,也不是偶函数.5分(Ⅱ)法一:证明:
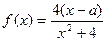 ,任取
,任取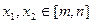 且
且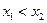 ,………6分
,………6分则
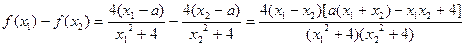 ………7分
………7分设
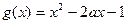 ,则
,则 即
即 ,…9分
,…9分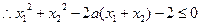 ,又
,又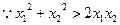 ………11分
………11分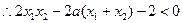 ,即
,即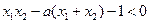 ………12分
………12分又
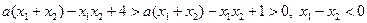 ,
,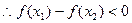 …13分
…13分即
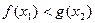 ,故
,故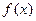 在区间
在区间 上是增函数. ………14分
上是增函数. ………14分法二:证明
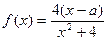 ,
, ……7分
……7分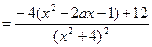 设
设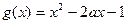 ,当
,当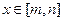 时,
时, 即
即

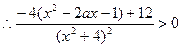 13分故
13分故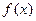 在区间
在区间 上是增函数.
上是增函数.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 x,求使f(x)=-
x,求使f(x)=-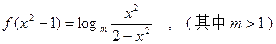
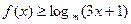
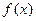 与
与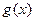 的定义域是
的定义域是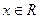 且
且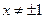 ,
,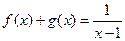 ,求
,求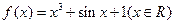 ,若
,若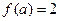 ,则
,则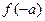 的值为( )
的值为( )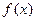 是偶函数,且当
是偶函数,且当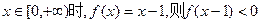 的解集是( )
的解集是( )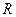 上的任意函数
上的任意函数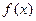 都可以表示成一个奇函数
都可以表示成一个奇函数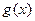 与一个
与一个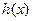 之和,如果
之和,如果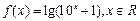 ,那么( )
,那么( )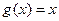 ,
,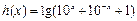
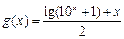 ,
,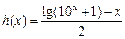
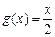 ,
,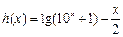
 ,
,