题目内容
已知函数f(x)的定义域为R,且满足f(x+2)=-f(x)?(1)求证:f(x)是周期函数;(2)若f(x)为奇函数,且当0≤x≤1时,f(x)= x,求使f(x)=-
x,求使f(x)=- 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数.
 x,求使f(x)=-
x,求使f(x)=- 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数.(Ⅰ)见解析 (Ⅱ) 502
(1)证明: ∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
∴f(x)是以4为周期的周期函数.
(2)解: 当0≤x≤1时,f(x)= x,设-1≤x≤0,则0≤-x≤1,∴f(-x)=
x,设-1≤x≤0,则0≤-x≤1,∴f(-x)= (-x)=-
(-x)=- x.
x.
∵f(x)是奇函数,∴f(-x)=-f(x),∴-f(x)=- x,即f(x)=
x,即f(x)=  x.
x.
故f(x)= x(-1≤x≤1) 又设1<x<3,则-1<x-2<1,
x(-1≤x≤1) 又设1<x<3,则-1<x-2<1,
∴f(x-2)= (x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
(x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
∴-f(x)= (x-2),∴f(x)=-
(x-2),∴f(x)=- (x-2)(1<x<3).
(x-2)(1<x<3).
∴f(x)=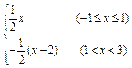 由f(x)=-
由f(x)=- ,解得x=-1.
,解得x=-1.
∵f(x)是以4为周期的周期函数.故f(x)=- 的所有x="4n-1" (n∈Z).
的所有x="4n-1" (n∈Z).
令0≤4n-1≤2 009,则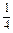 ≤n≤
≤n≤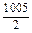 ,又∵n∈Z,∴1≤n≤502 (n∈Z),
,又∵n∈Z,∴1≤n≤502 (n∈Z),
∴在[0,2 009]上共有502个x使f(x)=- .
.
∴f(x)是以4为周期的周期函数.
(2)解: 当0≤x≤1时,f(x)=
 x,设-1≤x≤0,则0≤-x≤1,∴f(-x)=
x,设-1≤x≤0,则0≤-x≤1,∴f(-x)= (-x)=-
(-x)=- x.
x.∵f(x)是奇函数,∴f(-x)=-f(x),∴-f(x)=-
 x,即f(x)=
x,即f(x)=  x.
x. 故f(x)=
 x(-1≤x≤1) 又设1<x<3,则-1<x-2<1,
x(-1≤x≤1) 又设1<x<3,则-1<x-2<1,∴f(x-2)=
 (x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
(x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),∴-f(x)=
 (x-2),∴f(x)=-
(x-2),∴f(x)=- (x-2)(1<x<3).
(x-2)(1<x<3). ∴f(x)=
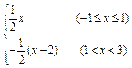 由f(x)=-
由f(x)=- ,解得x=-1.
,解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-
 的所有x="4n-1" (n∈Z).
的所有x="4n-1" (n∈Z). 令0≤4n-1≤2 009,则
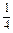 ≤n≤
≤n≤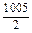 ,又∵n∈Z,∴1≤n≤502 (n∈Z),
,又∵n∈Z,∴1≤n≤502 (n∈Z),∴在[0,2 009]上共有502个x使f(x)=-
 .
.
练习册系列答案
相关题目
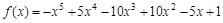 .求
.求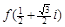 的值是( )
的值是( )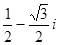
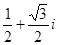
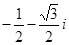

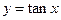 在其定义域内是增函数;②函数
在其定义域内是增函数;②函数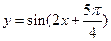 的图象关于直线
的图象关于直线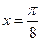 对称;③函数
对称;③函数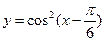 的最小正周期是2π;④函数
的最小正周期是2π;④函数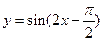 是偶函数.其中正确结论的序号是 .
是偶函数.其中正确结论的序号是 .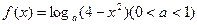
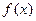 的奇偶性;
的奇偶性;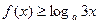 .
.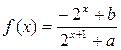
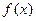 的解析式;
的解析式;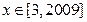 ,不等式
,不等式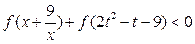 恒成立,求t
恒成立,求t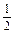 ≤a≤
≤a≤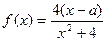 .
.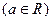 (Ⅰ)判断
(Ⅰ)判断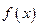 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程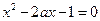 的两实根为
的两实根为 ,证明函数
,证明函数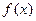 是
是 上的增函数.
上的增函数.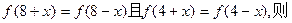
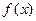 是( )
是( )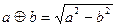 ,
, ,则
,则