题目内容
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1.若对任意a,b∈[-1,1],a+b≠0都有
>0.
(1)判断函数f(x)的单调性,并说明理由;
(2)解不等式f(x-
)+f(x-
)<0;
(3)若不等式f(x)+(2a-1)t-2≤0对所有x∈[-1,1]和a∈[-1,1]都恒成立,求实数t的取值范围.
| f(a)+f(b) |
| a+b |
(1)判断函数f(x)的单调性,并说明理由;
(2)解不等式f(x-
| 1 |
| 2 |
| 1 |
| 4 |
(3)若不等式f(x)+(2a-1)t-2≤0对所有x∈[-1,1]和a∈[-1,1]都恒成立,求实数t的取值范围.
(1)设任意x1,x2∈[-1,1],且x1<x2,
∵f(x)是定义在[-1,1]上的奇函数,
∴f(-x)=-f(x),
∴f(x1)-f(x2)=f(x1)+f(-x2),
∵对任意a,b∈[-1,1],a+b≠0都有
>0,
∴
>0,又x1<x2,则x1-x2<0,
∴f(x1)-f(x2)=f(x1)+f(-x2)=
(x1-x2)<0,
∴f(x1)-f(x2)<0,
∴f(x)在定义域[-1,1]上位增函数;
(2)∵函数f(x)为奇函数,
∴f(-x)=f(x),又不等式f(x-
)+f(x-
)<0,即f(x-
)<-f(x-
),
∴f(x-
)<-f(x-
)=f(
-x),
由(1)可知,f(x)在定义域[-1,1]上位增函数,
∴
,解得-
≤x<
,
∴不等式f(x-
)+f(x-
)<0的解集为{x|-
≤x<
};
(3)由(1)可知,f(x)在定义域[-1,1]上位增函数,
∴f(x)max=f(1),又f(1)=1,
∴f(x)max=1,
∵不等式f(x)+(2a-1)t-2≤0对所有x∈[-1,1]和a∈[-1,1]都恒成立,
∴f(x)max≤(1-2a)t+2对任意的a∈[-1,1]都恒成立,
∴1≤-2ta+t+2对任意的a∈[-1,1]都恒成立,
∴
,解得-
≤t≤1,
∴实数t的取值范围为-
≤t≤1.
∵f(x)是定义在[-1,1]上的奇函数,
∴f(-x)=-f(x),
∴f(x1)-f(x2)=f(x1)+f(-x2),
∵对任意a,b∈[-1,1],a+b≠0都有
| f(a)+f(b) |
| a+b |
∴
| f(x1)+f(-x2) |
| x1+(-x2) |
∴f(x1)-f(x2)=f(x1)+f(-x2)=
| f(x1)+f(-x2) |
| x1+(-x2) |
∴f(x1)-f(x2)<0,
∴f(x)在定义域[-1,1]上位增函数;
(2)∵函数f(x)为奇函数,
∴f(-x)=f(x),又不等式f(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴f(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
由(1)可知,f(x)在定义域[-1,1]上位增函数,
∴
|
| 1 |
| 2 |
| 3 |
| 8 |
∴不等式f(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
(3)由(1)可知,f(x)在定义域[-1,1]上位增函数,
∴f(x)max=f(1),又f(1)=1,
∴f(x)max=1,
∵不等式f(x)+(2a-1)t-2≤0对所有x∈[-1,1]和a∈[-1,1]都恒成立,
∴f(x)max≤(1-2a)t+2对任意的a∈[-1,1]都恒成立,
∴1≤-2ta+t+2对任意的a∈[-1,1]都恒成立,
∴
|
| 1 |
| 3 |
∴实数t的取值范围为-
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
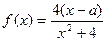 .
.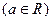 (Ⅰ)判断
(Ⅰ)判断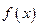 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程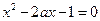 的两实根为
的两实根为 ,证明函数
,证明函数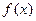 是
是 上的增函数.
上的增函数.