题目内容
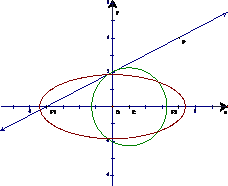
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
+
=1(a>b>0)有一个公共点A(3,1),F1,F2分别是椭圆的左右焦点,直线PF1与圆C相切.
(1)求m的值;
(2)求椭圆E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求m的值;
(2)求椭圆E的方程.

(1)点A(3,1)代入圆C方程,得(3-m)2+1=5,
∵m<3,∴m=1,;
(2)设直线PF1的斜率为k,则PF1:y=k(x-4)+4,即kx-y-4k+4=0,
因为直线PF1与圆C相切,所以
=
,解得k=
,或k=
.
当k=
时,直线PF1与x轴交点横坐标为
,不合题意,舍去.
当k=
时,直线PF1与x轴交点横坐标为-4,所以c=4,F1(-4,0),F2(4,0),
所以2a=|AF1|+|AF2|=5
+
=6
,a=3
,a2=18,b2=2,
所以椭圆E的方程为
+
=1.
∵m<3,∴m=1,;
(2)设直线PF1的斜率为k,则PF1:y=k(x-4)+4,即kx-y-4k+4=0,
因为直线PF1与圆C相切,所以
| |k-0-4k+4| | ||
|
| 5 |
| 11 |
| 2 |
| 1 |
| 2 |
当k=
| 11 |
| 2 |
| 36 |
| 11 |
当k=
| 1 |
| 2 |
所以2a=|AF1|+|AF2|=5
| 2 |
| 2 |
| 2 |
| 2 |
所以椭圆E的方程为
| x2 |
| 18 |
| y2 |
| 2 |

练习册系列答案
相关题目
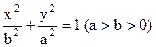 ,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
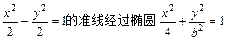 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()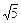
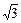
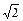


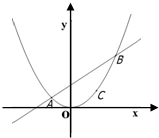
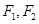 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以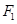 为顶点,
为顶点,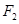 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足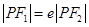 ,则e的值为( )
,则e的值为( )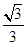 B.
B.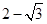 C.
C. 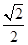 D.
D.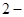
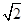

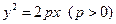 的焦点与双曲线
的焦点与双曲线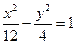 的右焦点重合,则
的右焦点重合,则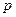 的值为C
的值为C .
. 
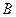 .
. 
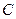 .
. 
 .
.