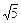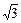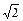题目内容
已知椭圆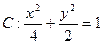 和圆
和圆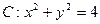 ,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点
,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点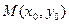 在直线
在直线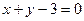 上,若存在点
上,若存在点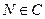 ,使得
,使得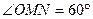 (O为坐标原点),求
(O为坐标原点),求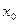 的取值范围。
的取值范围。
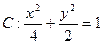 和圆
和圆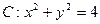 ,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点
,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。 (2)设点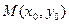 在直线
在直线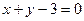 上,若存在点
上,若存在点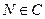 ,使得
,使得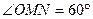 (O为坐标原点),求
(O为坐标原点),求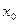 的取值范围。
的取值范围。(Ⅰ) 直线P与圆C相切 (Ⅱ) 

(1)直线P与圆C相切。…1分
证明如下:易得椭圆C1的右焦点为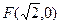 ,右准线为
,右准线为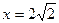 …………2分
…………2分
设点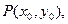 则有
则有 ,又
,又
∴直线PQ的方程为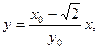 令
令 ,
,
即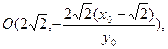
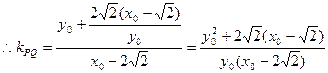
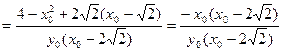
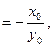 又
又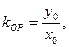 ………5分
………5分
于是有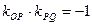 ,故OP⊥PQ,
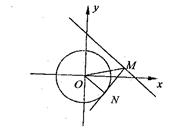
,故OP⊥PQ,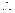 直线P与圆C相切(3)如图,设
直线P与圆C相切(3)如图,设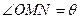 ,则
,则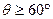 ,
,
即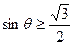 ,即
,即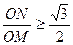 ,而ON=2,
,而ON=2,

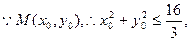
又由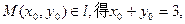
 于是有
于是有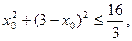 …2分
…2分
整理,得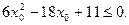 解得
解得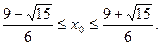
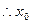 的取值范围是
的取值范围是
证明如下:易得椭圆C1的右焦点为
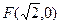 ,右准线为
,右准线为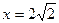 …………2分
…………2分设点
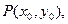 则有
则有 ,又
,又
∴直线PQ的方程为
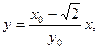 令
令 ,
,即
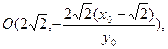
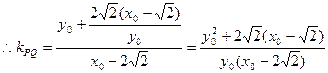
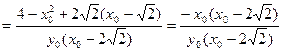
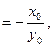 又
又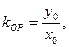 ………5分
………5分
|
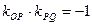 ,故OP⊥PQ,
,故OP⊥PQ, 直线P与圆C相切(3)如图,设
直线P与圆C相切(3)如图,设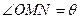 ,则
,则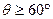 ,
,即
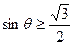 ,即
,即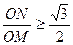 ,而ON=2,
,而ON=2,
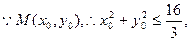
又由
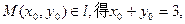
 于是有
于是有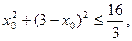 …2分
…2分整理,得
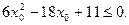 解得
解得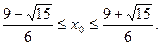
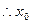 的取值范围是
的取值范围是

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
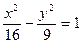
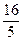
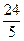
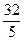
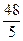
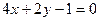 ;②
;② 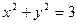 ;③
;③ 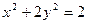 ;
;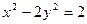 .其中与直线2 x + y +3=0有交点的所有曲线是
.其中与直线2 x + y +3=0有交点的所有曲线是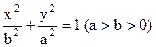 ,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
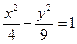 上的两个动点,满足
上的两个动点,满足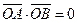 。(Ⅰ)求证:
。(Ⅰ)求证: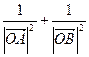 为定值; (Ⅱ)动点P在线段AB上,满足
为定值; (Ⅱ)动点P在线段AB上,满足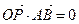 ,求证:点P在定圆上.
,求证:点P在定圆上. ,y
,y )、B(x
)、B(x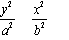 (a > b > 0) 上的两点,
(a > b > 0) 上的两点,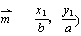 ,
,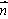 = (
= (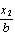 ,
,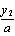 ),且满足
),且满足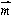 ·
·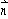 = 0,椭圆的离心率e =
= 0,椭圆的离心率e = 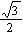 ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.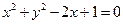 表示的图形是圆;②椭圆椭圆
表示的图形是圆;②椭圆椭圆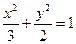 的离心率
的离心率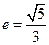 ;③抛物线
;③抛物线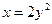 的准线的方程是
的准线的方程是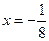 ;④双曲线
;④双曲线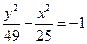 的渐近线方程是
的渐近线方程是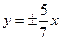 。其中所有不正确命题的序号是 。
。其中所有不正确命题的序号是 。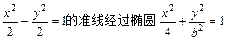 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()