题目内容
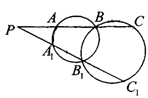
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,则BC的长为 _________ .


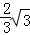
连接OD、BD,
∵DE⊥AB,垂足为E,且E是OB的中点
∴可得等腰三角形BOD是等边三角形,
∵在直角三角形OCD中,CD=2,
∴可得OD=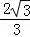 ,
,
∵CD是圆O的切线,∴由切割线定理得,
∴CD2=CB×CA,
即4=CB×(CB+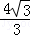 )
)
∴BC=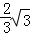 ,
,
故填: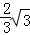 .
.
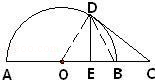
∵DE⊥AB,垂足为E,且E是OB的中点
∴可得等腰三角形BOD是等边三角形,
∵在直角三角形OCD中,CD=2,
∴可得OD=
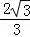 ,
,∵CD是圆O的切线,∴由切割线定理得,
∴CD2=CB×CA,
即4=CB×(CB+
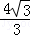 )
)∴BC=
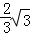 ,
,故填:
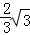 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 是⊙
是⊙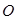 的直径,
的直径,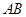 是⊙
是⊙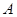 为切点,⊙
为切点,⊙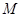 、
、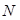 ,直线
,直线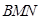 交
交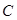 ,
,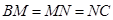 ,
,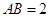 ,则⊙
,则⊙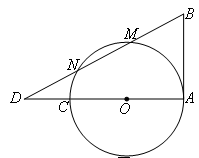


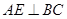 ,
,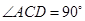 ,且AB=6,AC=4,AD=12,则BE= .
,且AB=6,AC=4,AD=12,则BE= .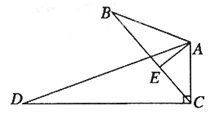
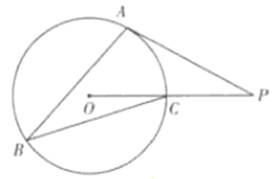

 为⊙
为⊙ 的两条切线,切点分别为
的两条切线,切点分别为 ,过
,过 的中点
的中点 作割线交⊙
作割线交⊙ 两点,若
两点,若 则
则 .
.
 切圆
切圆 于点
于点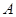 ,割线
,割线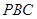 经过圆心
经过圆心 ,
, 绕点
绕点 到
到 ,则
,则 的长为 .
的长为 .
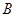 、
、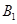 ,直线
,直线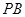 与
与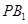 分别与两圆交于点
分别与两圆交于点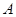 、
、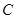 和
和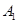 、
、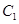 ,
,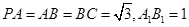 ,则
,则 .
.